【鞅与停时】Snell包络与37法则

秘书问题与37%法则

考虑一个包含 $N$ 个候选人的池子，他们的能力用未知的数序列 ${a_{1} > a_{2} > \dots > a_{N}}$ 表示，从最好到最差。这些候选人被依次随机面试并当场给出面试结果，即 ${Y_{1}, Y_{2}, \dots, Y_{N}}$ 是 ${a_{1}, a_{2}, \dots, a_{N}}$ 的一个随机排列，所有 $N!$ 种排列的可能性都是相等的。被拒绝的候选人不能被重新召回。
面试过程中无法直接观察到候选人的实际能力值 ${Y_{1}, Y_{2}, \dots, Y_{N}}$ ,只能观察到相对排名 $X_{n}$ ,即第 $n$ 个候选人在前 $n$ 个面试者中的排名。相对排名 $X_{n}$ 定义为：

X_{n} ≐ \sum_{k = 1}^{n} 1_{{Y_{n} \leq Y_{k}}}

那么如何基于相对排名的信息 ${X_{1}, X_{2}, \dots, X_{n}}$ 选择一个停止时间 $τ$ ，使得选中最优秀候选人的概率 $P (Y_{τ} = a_{1})$ 最大化？

首先，注意到 ${X_{1}, X_{2}, \dots, X_{N}}$ 是独立的随机变量且均服从等概率分布

P (X_{n} = 1) = P (X_{n} = 2) = \dots = P (X_{n} = n) = 1 / n, n = {1, \dots, N}

$Y_{n}$ 不是基于 ${X_{1}, X_{2}, \dots, X_{n}}$ 可测的，那么就要将选择最佳候选人的概率通过相对排名 $X_{n}$ 相关的条件概率表示。令 $f_{n} (X_{n}) = P (Y_{n} = a_{1} | X_{1}, \dots, X_{n})$ ，那么有

f_{n} (x) ≐ {\begin{array}{cc} n / N & ; if x = 1 \\ 0 & ; if x > 1 \end{array}

，给出了在面试第 $n$ 个面试者时给出相对排名的最佳候选人概率。
那么可以得到某时刻停止时的最佳候选人概率（期望收益）与 $f_{n} (x)$ 关系

\begin{aligned} P (Y_{τ} = a_{1}) & = \sum_{k = 1}^{n} E [1_{{Y_{n} = a_{1}}} 1_{{τ = n}}] \\ = \sum_{k = 1}^{n} E [E [1_{{Y_{n} = a_{1}}} 1_{{τ = n}} | X_{1}, \dots, X_{n}]] \\ = \sum_{k = 1}^{n} E [1_{{τ = n}} E [1_{{Y_{n} = a_{1}}} | X_{1}, \dots, X_{n}]] \\ = \sum_{k = 1}^{n} E [\begin{array}{c} 1_{{τ = n}} f_{n} (X_{n}) \end{array}] \\ = E f_{τ} (X_{τ}) \end{aligned}

动态规划方程（DPE）有

\begin{aligned} V_{n} (x) & = max {f_{n} (x), \frac{1}{n + 1} \sum_{k = 1}^{n + 1} V_{n + 1} (k)} \\ V_{N} (x) & = f_{N} (x) \end{aligned}

其中：

$V_{n} (x)$ 是时刻 n下取值 $X_{n} = x$ 时能够获得的最大期望收益，即 $V_{n} (x) = max {立即停止的收益, 继续观察的期望收益}$
$f_{n} (x)$ ：立即停止的收益，即选择当前候选人。
$\frac{1}{n + 1} \sum_{k = 1}^{n + 1} V_{n + 1} (k)$ ：继续观察的期望收益。因为 $X_{n}$ 是服从一个均匀分布，因此继续观察的期望即不同 k 对应的 value 的均值。
【重要观察】

$V_{n}$ 是递减的
如果 $V_{n} (X_{n}) = f_{n} (X_{n})$ ，说明当前停止时最优的，后续策略也是最优的（贝尔曼最优性条件）

\begin{matrix} σ^{*} ≐ inf {n \geq 1 : V_{n} (X_{n}) = f_{n} (X_{n})} \\ sup_{τ} P (Y_{τ} = a_{1}) = V_{1} (1) \end{matrix}

由 N 递减递推可得

V_{n} (x) = {\begin{cases} f_{n} (x), if \frac{n}{N} (\frac{1}{N - 1} + \dots + \frac{1}{n}) < \frac{n}{N} \\ \frac{1}{n + 1} \sum_{k = 1}^{n + 1} V_{n + 1} (k), else \end{cases}

设 $m (N)$ 即不等式恰好变号的 $n$ 即 $\sum_{k = m (N)}^{N - 1} \frac{1}{k} \leq 1 < \sum_{k = m (N) - 1}^{N - 1} \frac{1}{k}$ ，那么

V_{n} (x) = {\begin{array}{ccc} n / N & ; & if x = 1 \\ \frac{n}{N} [\frac{1}{N - 1} + \dots + \frac{1}{n}] & ; & if x > 1 \end{array} n \geq m (N)

V_{n} (x) = \frac{m (N) - 1}{N} [\frac{1}{N - 1} + \dots + \frac{1}{m (N) - 1}]; n < m (N)

最优停时即为 $σ^{*} = inf {n \geq m (N) : X_{n} = 1}$

sup_{τ} P (Y_{τ} = a_{1}) = V_{1} (1) = \frac{m (N) - 1}{N} [\frac{1}{N - 1} + \dots + \frac{1}{m (N) - 1}]

【 $N \to \infty$ 】

\frac{M (n)}{n} \sum_{k = M (n) + 1}^{n} \frac{1}{k - 1} \approx \frac{M (n)}{n} \int_{M (n)}^{n - 1} \frac{1}{x} d x = \frac{M (n)}{n} \ln (\frac{n - 1}{M (n)}) \approx \frac{M (n)}{n} \ln (\frac{n}{M (n)})

上式=1 即为 $x \ln x$ 极点值， $M (N) / N = 1 / e \approx 37 %$

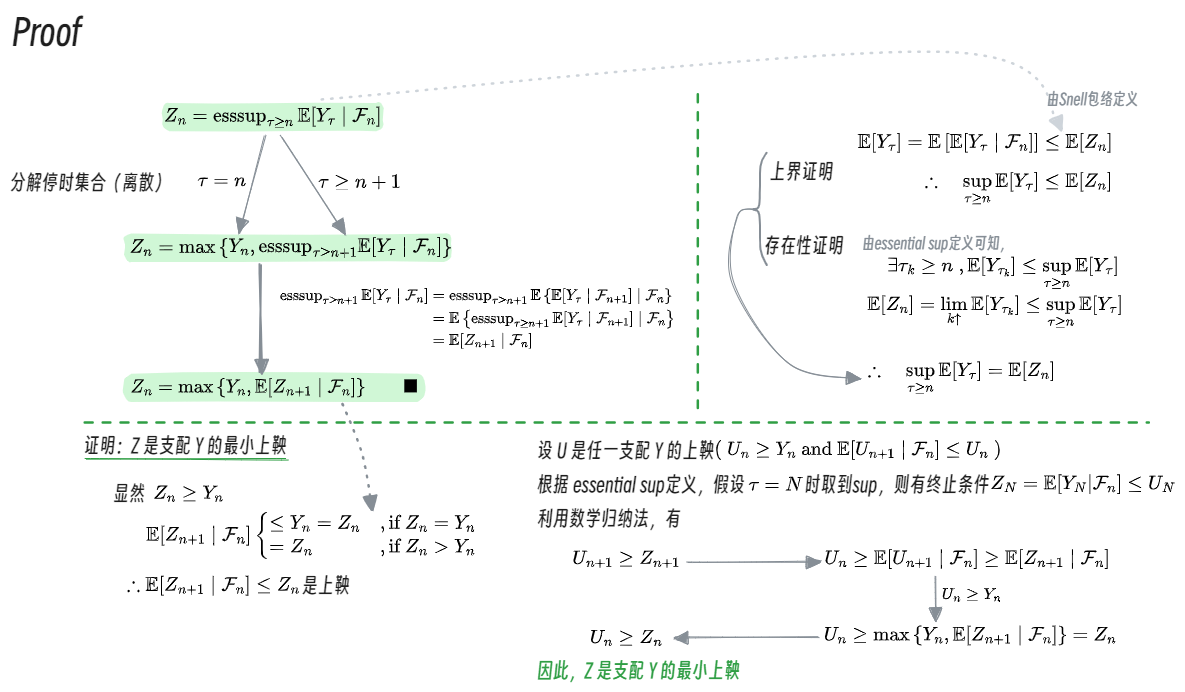
Snell Envelops

通过上述秘书问题可以看出其中的 $V_{n}$ 其实就是截止在时刻 n 未来策略收益的最小上界e（ssential supremum），把可以表述这种性质的函数定义为 Snell 包络。

Snell Envelope

The Snell envelope is defined as the process $Z = {Z_{n}}$ given by^[1]

Z_{n} ≐ {esssup}_{τ \geq n} E [Y_{τ} | F_{n}]

其中 $Y$ 为收益函数， $τ$ 为停时。

随机过程 $Z$ 满足动态规划

Z_{n} = max {Y_{n}, E [Z_{n + 1} | F_{n}]}

$sup_{τ \geq n} E [Y_{τ}] = E [Z_{n}]$
Snell 包络是支配 $Y$ 的最小上鞅

optimal stopping time

$v_{0} = sup_{τ} E [Y_{τ}]$ is attained if and only if the stopping time

σ^{*} ≐ inf {n \geq 0 : Z_{n} = Y_{n}}

is finite with probability one. In this case, $σ^{*}$ is indeed optimal.

定理表明当且仅当停时 $σ^{*}$ 几乎必然有限时，最优停止问题的上确界可被达到，且是最优停时。

Proof

若 $σ^{*}$ 几乎必然有限，则 $σ^{*}$ 最优
构造截断停时 $d$ ，保证其有限性

\begin{aligned} E [Z_{σ^{*} \land (n + 1)} | F_{n}] & = 1_{{σ^{*} \leq n}} Z_{σ^{*}} + 1_{{σ^{*} > n}} \cdot E [Z_{n + 1} | F_{n}] \\ = 1_{{σ^{*} \leq n}} Z_{σ^{*}} + 1_{{σ^{*} > n}} \cdot Z_{n} \\ = Z_{σ^{*} \land n} \end{aligned}

可证 ${Z_{σ^{*} \land n} : n \geq 0}$ 是鞅。因为 $lim_{n \to \infty} E [Z_{σ^{*} \land n}] = E [Z_{σ^{*}}]$ ， $E [Z_{σ^{*} \land n}] = E [Z_{0}]$ ，有（最后一个等号一句 $σ^{*}$ 定义）

sup_{τ \geq n} E [Y_{τ}] = E [Z_{0}] = E [Z_{σ^{*}}] = E [Y_{σ^{*}}]

说明 $σ^{*}$ 达到上确界，optimal
2. 若存在最优停时 $ρ$ ，则 $σ^{*}$ 必有限
假设有最优停时，满足 $sup_{τ \geq n} E [Y_{τ}] = E [Y_{ρ}]$ 。
根据 Snell 包络性质， $Y_{ρ} \leq Z_{ρ} a . s .$ ，那么根据 Z 的上鞅性质，

E [Y_{ρ}] \leq E [Z_{ρ}] \leq E [Z_{0}] = sup_{τ \geq n} E [Y_{τ}] = E [Y_{ρ}]

因此结合 $Y_{ρ} \leq Z_{ρ}$ 得到 $Z_{ρ} = Y_{ρ} a . s .$ 进而 $σ^{*} \leq ρ$ 。由于 $ρ$ 的存在性，几乎必然有 $σ^{*}$ 有限。

Notes on Snell Envelops and Examples ↩︎