【鞅与停时】Martingale

#概率论 #鞅

因为看的文献涉及到诸多关于停时相关的定理，因而关注了下鞅与停时这部分的内容。重点关注鞅的构造以及停时相关应用，其分析性质不多赘述。

鞅

鞅的提出，其实就是为了描述一个赌博的博弈模型。简单来说，具备鞅性质的赌博过程，包含了赌博输赢，输多少赢多少，怎么输怎么赢的一切信息。而如果要让鞅具备如此强大的能力，自然就需要让它具备一定的抽象性，一定的铺垫。

Martingale, super-Martingale, sub-Martingale

对于一个随机变量 $M_{n}$ ， ${X_{n}}$ 是一个随机过程。如果满足

$M_{n}$ 仅仅与 $X_{0}, \dots, X_{n}$ 有关。
$E (M_{n} + 1 | X_{n}, \dots, X_{0}) = M_{n}$
则称它是一个关于 $X_{n}$ 的鞅。如果第2个式子的符号为 $\leq$ ，那么称它为上鞅。如果为 $\geq$ ，那么称它为下鞅。

定义中第二点即 $\forall x_{0}, \dots, x_{n}, E (M_{n + 1} | X_{n} = x_{n}, \dots, X_{0} = x_{0}) = M_{n}$

上鞅与下鞅的定义与直觉中的“递增/递减”恰好相反，主要和后面的上调和和下调和函数有关

鞅与赌博问题

鞅其实是衡量“赌注的变化趋势”的，这里详细介绍一下背景

赌博游戏

考虑一个赌博游戏，一开始的赌注为1。如果获胜，则获得赌注，且下一局的赌注重置为1。如果输了，则失去这个赌注，且下一局的赌注翻倍。假设输赢的概率相等，问这一个赌博问题是否存在好的策略。

直觉误区：只要赢一次，就能覆盖之前的所有损失并净赚1（ $- 1 - 2 \dots - 2^{n} + 2^{n + 1}$ ）；但关键在于假设玩家有无限资金和无限时间，可以持续下注直至获胜。
若资金或时间有限情况下，通过分析收益的期望容易得知该游戏并没有什么收益（通过输赢概率相等也容易直观得出）
【鞅的角度】定义 $X_{n} = \pm 1$ 为每局的胜负；鞅 $M_{n} = \sum_{i = 1}^{n} X_{n}$ ，每一次赌注为 $H_{n} = H_{n - 1}, 2 H_{n - 1}$ ；总收益为

W_{n} = W_{0} + \sum_{m = 1}^{n} H_{m} (M_{m} - M_{m - 1})

Proposition

设 $M_{n}$ 是一个关于 $X_{n}$ 的鞅， $H_{n}$ 是一个仅仅与 $X_{0}, \dots, X_{n - 1}$ 有关的量，且 $0 \leq H_{n} \leq c_{n}$ ，那么 $W_{n}$ 就是一个鞅。

上述推论通过推出 $E (W_{n + 1} - W_{n} | X_{0}, \dots, X_{n}) = 0$ 易证，“资金或时间有限”在后面的停时理论也有所对应

就是说，只要这个游戏本身是公平的，无论怎样改变策略，期望的收益都不会有变。且条件改成下鞅或者上鞅同理。比方说对于下鞅，只要游戏本身是对玩家不利的，期望的收益都会对玩家不利。

常见的鞅

随机游走

考虑一个随机游走过程，即

S_{n} = S_{0} + \sum_{i = 1}^{n} X_{i}

其中 $X_{1}, X_{2}, \dots$ 独立同分布，满足

E (X_{i}) = μ, Var (X_{i}) = σ^{2}

$S_{n} - n μ$ 是关于 ${X_{n}}$ 的鞅。
$S_{n}$ 是上鞅还是下鞅，取决于 $μ$ 的正负。
$(S_{n} - n μ)^{2} - n σ^{2}$ 是关于 ${X_{n}}$ 的鞅。

Proof

令 $Y_{n} = S_{n} - n μ$ ，即要证 $E [Y_{n + 1} ∣ F_{n}] = Y_{n}, F_{n} = σ (X_{0}, X_{1}, \dots, X_{n})$

\begin{aligned} E [Y_{n + 1} ∣ F_{n}] & = E [S_{n + 1} - (n + 1) μ ∣ F_{n}] \\ = E [S_{n} + X_{n + 1} - (n + 1) μ ∣ F_{n}] \\ = E [S_{n} - n μ ∣ F_{n}] + E [X_{n + 1} ∣ F_{n}] - μ \\ = Y_{n} . \end{aligned}

通过下式易证

E [S_{n + 1} - S_{n} ∣ F_{n}] = E [X_{n + 1} ∣ F_{n}] = μ

利用 $E [X_{n + 1} ∣ F_{n}] = μ$ 和 $Var (X_{n + 1}) = σ^{2}$ ，展开 $Z_{n + 1}$ 的条件期望

\begin{aligned} E {[(S_{n + 1} - (n + 1) μ)^{2} - (n + 1) σ^{2}] - [(S_{n} - n μ)^{2} - n σ^{2}] ∣ F_{n}} \\ = E {2 (S_{n} - n μ) (X_{n + 1} - μ) + (X_{n + 1} - μ)^{2} - σ^{2} ∣ F_{n}} \\ = 2 (S_{n} - n μ) E {X_{n + 1} - μ ∣ F_{n}} + E {(X_{n + 1} - μ)^{2}} - σ^{2} \\ = 0 \end{aligned}

（第 2 个等号注意到 $S_{n} - n μ$ 在已知 $F_{n}$ 时为已知量）

Product Martingale

设 $X_{1}, X_{2}, \dots$ 为独立的随机变量，并且 $E (X_{i}) = 1$ ，那么 $M_{n} = M_{0} X_{1} \dots X_{n}$ 是一个关于 $X_{n}$ 的鞅。

乘积鞅衡量了随机过程的乘积累积效应

$\begin{aligned} E (M_{n + 1} | X_{0}, \dots, X_{n}) = E (M_{n} X_{n + 1} | X_{0}, \dots, X_{n}) = M_{n} E (X_{n + 1}) = M_{n} \end{aligned}$ 易证

Exponential Martingale

设 $X_{1}, X_{2}, \dots$ 是独立同分布的随机变量，且 $ϕ (θ) = E (e^{θ X_{1}}) < \infty$ ， $S_{n} = S_{0} + \sum_{k = 1}^{n} X_{k}$ 。则 $M_{n} = \exp (θ S_{n}) / ϕ (θ)^{n}$ 是一个指数鞅。

上述类型的鞅重点在于如何构造鞅便于应用后面鞅的性质。

指数鞅的一个例子

$P (X_{i} = 1) = p, P (X_{i} = - 1) = 1 - p$ ，则 ${(\frac{1 - p}{p})}^{S_{n}}$ is martingale.
【证明】不妨令 $ϕ (θ) = 1$ 可简化指数鞅的表达且有界，则有

E (e^{θ X_{1}}) = e^{θ} p + e^{- θ} (1 - p) = 1 ⟹ θ = \ln (\frac{1 - p}{p})

则此时即 $\exp (θ S_{n}) / ϕ (θ)^{n} = {(\frac{1 - p}{p})}^{S_{n}}$ 是一个鞅

连续鞅

适应性

随机过程 ${X (t), t \geq 0}$ 称为适应的，若对 $\forall t \geq 0$ ，随机变量 $X_{t}$ 是 $F_{t}$ 可测的。
即，对任何 Borel集 $B \in B (R)$ ，事件 ${X_{t} \in B}$ 必须属于 $F_{t}$

适应性作用在于保证了过程的当前值完全由历史信息决定，不依赖未来。也可参考关于sigma代数部分进一步理解

连续鞅

一个适应过程 ${X_{t}, t ⩾ 0}$ 称为关于 ${F_{t}}$ 的（连续）鞅，如果

每个 $X_{t}$ 可积，即 $E (| X_{t} |) < \infty;$
对一切 $0 ⩽ s < t$ ,有

E (X_{t} | F_{s}) = X_{s} a. s.

当 $F_{t} = σ (X_{u}, 0 ⩽ u ⩽ t)$ , 即包含一切形如 ${X_{s} \leq s} (s \leq t, x \in R)$ 的事件的最小 $σ$ 代数，那么对关于 ${F_{t}}$ 的鞅 ${X_{t}, t ⩾ 0}$ 有

E (X_{t} | X_{u}, 0 ⩽ u ⩽ s) = X_{s} a . s .

鞅的极限性质

鞅收敛定理

设 ${M_{n}, n ⩾ 0}$ 是一个关于 ${X_{n}, n ⩾ 0}$ 的鞅，并且存在常数 $C < \infty$ ,使得 $\forall n, E [| M_{n} |] < C$ ,则当 $n \to \infty$ ，序列 ${M_{n}}$ 收敛到一个随机变量 $M_{\infty}$ 。

以波利亚之瓮（Polya's Urn）为例介绍

波利亚之瓮（Polya's Urn）

考虑一个波利亚的瓮，一开始的时候，瓮里有 $k$ 个球，它们中间有红球有蓝球，但是保证这 $k$ 个球里至少有1个红球和1个蓝球。每一次的时候，都会等概率的从中取出一个球，放回之后，再放进这一个颜色的一个球，使得总数变成 $k + 1$ 个。定义 $X_{n}$ 是红球的占比，那么极限情况下， $X_{n}$ 服从什么样的分布？

注意到

可知 $X_{n}$ 是一个鞅。
考虑最简单的情况： $k = 2, X_{0} = 1 / 2$
即转化为一个排列组合问题， $n$ 次放球无论顺序最后有 $j$ 个红球的概率均为 $\frac{1 \dots (j - 1) \cdot 1 \dots (n - j + 1)}{2 \dots (n + 1)}$

P (X_{n} = \frac{j}{n + 2}) = C_{n}^{j - 1} \frac{j! \cdot (n - j + 2)!}{(n + 1)!} = \frac{1}{n + 1}

即说明极限分布为均匀分布 $X_{\infty} \sim U (0, 1)$

当 $k = 3, X_{0} = 1 / 3$ 时，仍可算得 $f (x) = 2 - 2 x, 0 < x < 1$
$P (X_{n} = \frac{j}{n + 3}) = C_{n}^{j - 1} \frac{1 \dots (j - 1) \cdot 2 \dots (n - j + 2)}{3 \dots (n + 2)}$

关于 $σ$ 代数

$σ$ 代数用于严格化定义概率空间 $(Ω, F, P)$

度量“事件发生的可能性”的大小，对应到测度论就是“集合的测度”，定义测度同时保证集合的可列次交、并、差、余、极限的运算封闭

σ

代数，可测空间

(Ω, F)

设 $Ω$ 是一个样本空间（或任意一个集合）， $F$ 是 $Ω$ 的某些子集组成的集合族。若满足以下条件：

$Ω \in F$ ；
若 $A \in F$ ，则其补集 $A^{c} = Ω ∖ A \in F$ ；
若 $A_{n} \in F$ （ $n = 1, 2, \dots$ ），则并集 $⋃_{n = 1}^{\infty} A_{n} \in F$
则称 $F$ 为 $σ$ 代数，称 $(Ω, F)$ 为 可测空间，并称 $F$ 中的元素为事件

$σ$ 代数满足：
- 对有限交、有限并封闭
- 对可列个无限交/并封闭
- 对集合的上下极限封闭
生成 $σ$ 代数
存在包含 $C$ (任一非空集类)的最小 $σ$ 代数，称为生成的最小 $σ$ 代数

σ (C) = ⋂ {H | H 为包含 C 的 σ 代数}

概率，概率空间

设 $(Ω, F)$ 为可测空间，定义在 $F$ 上的实值函数 $P$ 满足以下条件时，称 $P$ 是 $(Ω, F)$ 上的概率测度，并称 $(Ω, F, P)$ 为概率空间， $P (A)$ 为事件 $A$ 的概率。

非负性： $\forall A \in F, 0 \leq P (A) \leq 1$
规范性： $P (Ω) = 1$
可列可加性：对 $F$ 中两两不相容的事件 $A_{1}, A_{2}, \dots$ ，有

P (⋃_{n = 1}^{\infty} A_{n}) = \sum_{n = 1}^{\infty} P (A_{n})

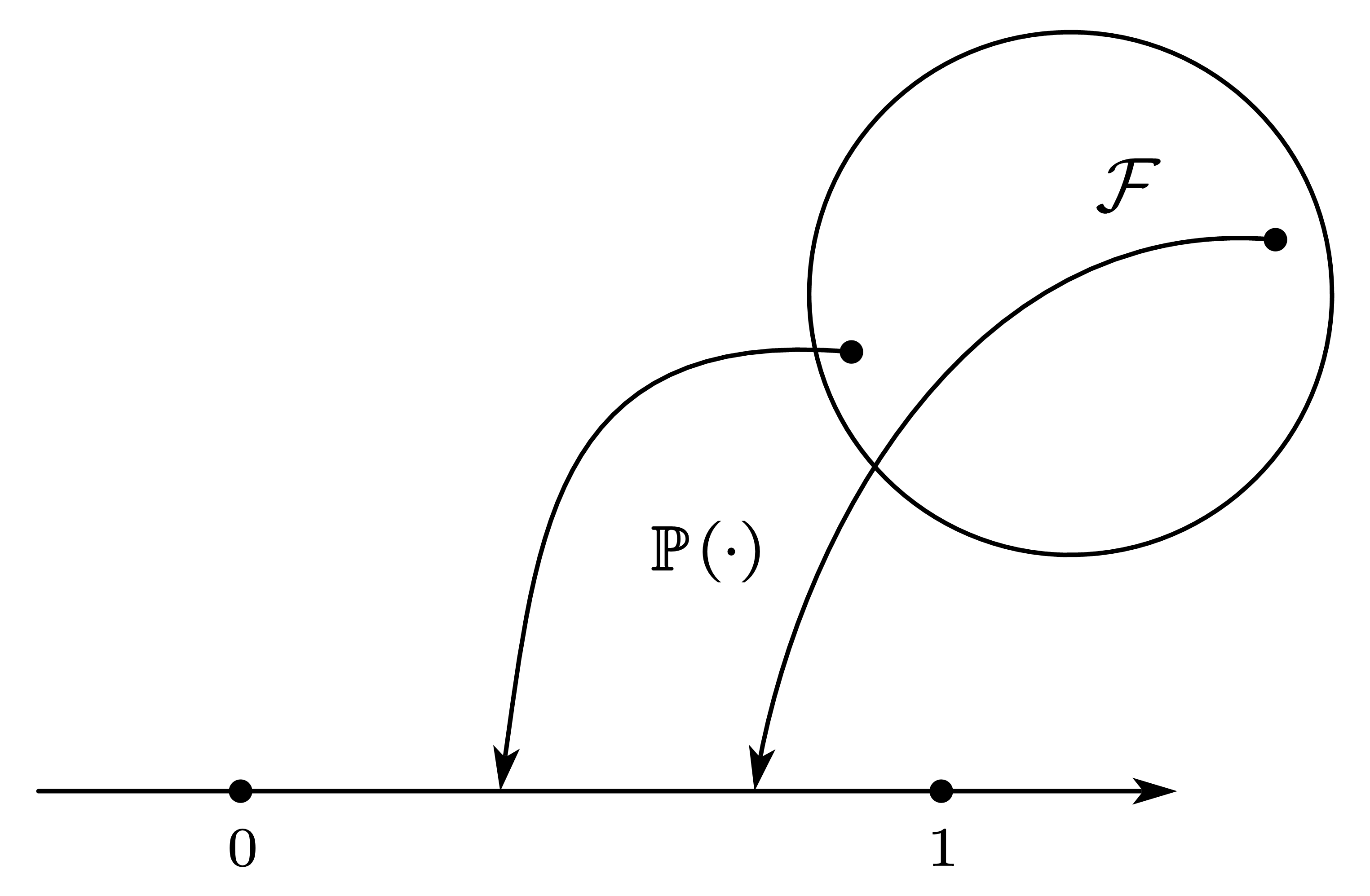
【这里 $F$ ( $σ$ 代数) 的作用？】从样本点定义到（复杂）事件的概率，只有事件 $A \in F$ 时 $P (A)$ 被定义

若定义 $Ω = {1, 2, 3, 4}$ ， $F_{1} = {Ω, \emptyset, {1, 2}, {3}, {4}}$ , $P {{1, 2}} = \frac{1}{2}, P {{3}} = P {{4}} = \frac{1}{4}, P (\emptyset) = 0, P {Ω} = 1$ 。此时 $P {{1}}$ 是没有意义的虽然 1 在样本空间中

从 $σ$ 代数到Borel 集

Borel Feild 就是 Borel $σ$ 代数，表示实数轴上的 $σ$ 代数，可由实数轴的所有开集（或所有 $(- \infty, a]$ 区间）生成 $σ$ 代数
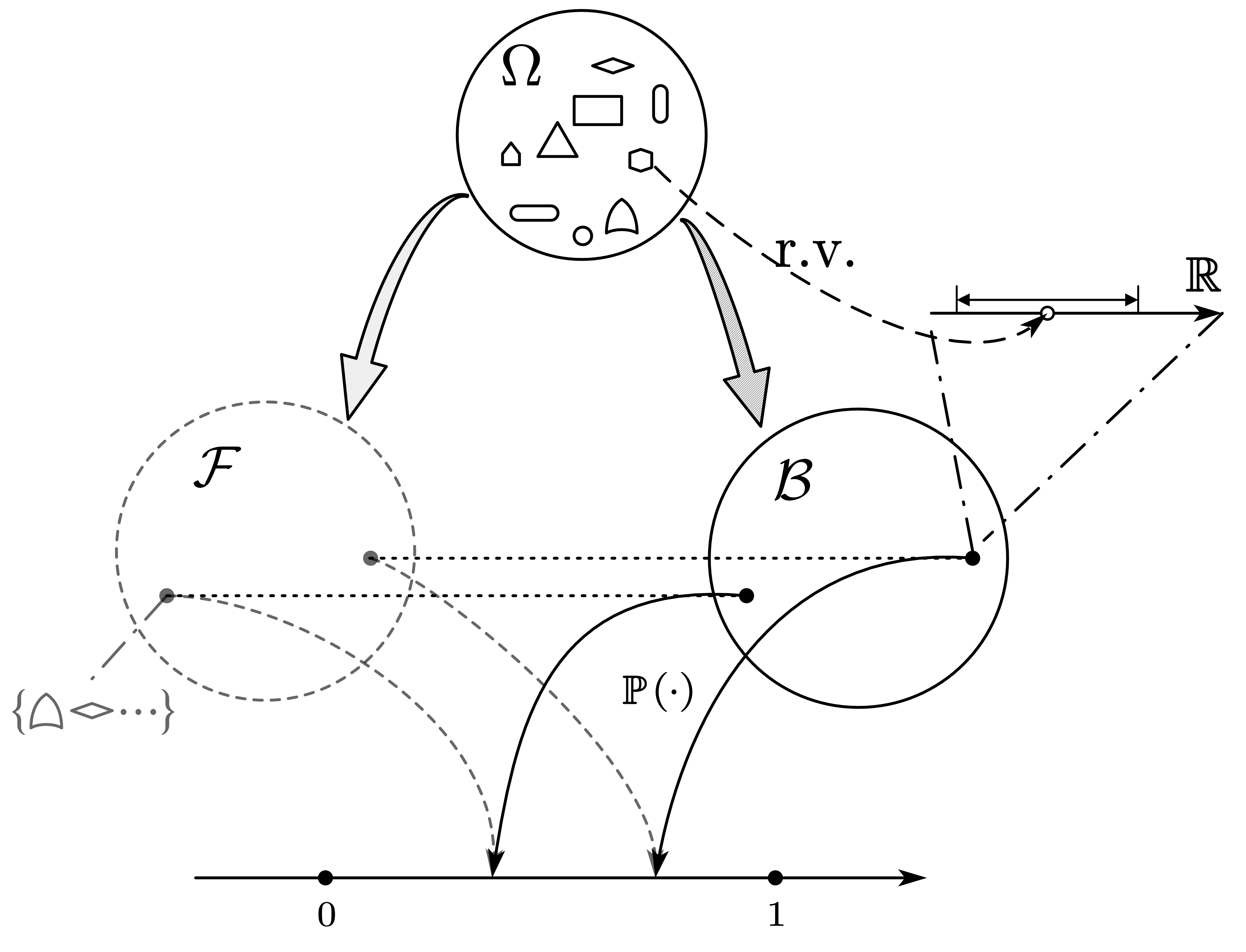
概率论中的随机变量，对应测度论中的可测函数，即 $(Ω, F) \to (R, B)$ 的可测映射。因此随机变量对应的测度论语言定义即

Def

设 $(Ω, F, P)$ 为概率测度空间，若对实数轴上Borel $σ$ 代数中的任一集合（称为Borel集） $B$ ，都有 ${w \in Ω : X (w) \in B} \in F$ ，则称 $X (w)$ 为随机变量。

根据上述定义可知 $P {w \in Ω : X (w) \in B}$ 有意义（因其属于 $F$ ），概率中即简记为 $P {X \in B}$
特别地若取 $B = (- \infty, x)$ ，则

P {X \in B} = P {X \leq x} := F (x)

注意其中的 $w \in Ω$ 而非 $\in F$ ， $w$ 是样本点（通过随机变量与数对应）而非事件
如上例中 $Ω = {1, 2, 3, 4}$ ， $1 \in Ω$ 是样本点而 ${1} \in F$ 为事件

其他

在鞅的定义/构造等相关公式中经常出现 $σ$ 代数的身影，主要是为了严格化完备化相关定义；一般工程论文中出现的 $E {\cdot | σ (X_{1}, \dots, X_{n})}$ 可直接视为 $E {\cdot | X_{1}, \dots, X_{n}}$

σ

子代数流

在完备的概率空间 $(Ω, F, P)$ 上，称 ${F_{n}, n \geq 0}$ 是 $σ$ 子代数流，如果 ${F_{n}, n ⩾ 0}$ 是 $F$ 上的一列 $σ$ 子代数，并且使得 $F_{1} \subset F_{2} \subset \dots \subset F_{n}$ , $n ⩾ 0$ ．