【随机过程】布朗运动

Brown 运动与维纳过程

Brown 运动(Brownian Motion)又称为 Wiener 过程(Weiner Process)，是对称随机游走的连续化。

从对称随机游动到布朗运动

考虑对称随机游动过程：

X_{i} = {\begin{cases} + 1, & 如果长度为 Δ x 的第 i 步是向右的 \\ - 1, & 如果长度为 Δ x 的第 i 步是向左的 \end{cases}

记 $X (t) = Δ x (X_{1} + \dots + X_{⌊ t / Δ t ⌋})$ 为时刻 $t$ 的位置,，假定 $X_{i}$ 独立且

P {X_{i} = 1} = P {X_{i} = - 1} = \frac{1}{2}

因此

E [X (t)] = 0, Var (X (t)) = (Δ x)^{2} [\frac{t}{Δ t}]

如果令 $Δ x = σ \sqrt{Δ t}, Δ t \to 0$ ，即可认为 $X (t)$ 为布朗运动

布朗运动过程（维纳过程）

如果随机过程 ${X (t), t ⩾ 0}$ 满足一下条件，则称其为布朗运动过程。

$X (0) = 0;$
${X (t), t ⩾ 0}$ 有平稳独立的增量；
对于任意 $t > 0, X (t)$ 是均值为 0，方差为 $σ^{2} t$ 的正态随机变量

布朗运动起源

布朗运动过程，有时称为维纳过程。这个现象，以发现它的英国植物学家 Robert Brown 的名字命名，是由全部浸没在液体或气体中的微粒展示的运动。布朗运动现象的第一个解释由爱因斯坦在 1905 年给出。然而，潜在于布朗运动的随机过程的上述简明定义是由维纳在 1918 年开始的一系列文章中给出的。

性质 2 平稳独立增量说明 $X (t_{n}) - X (t_{n - 1}), X (t_{n - 1}) - X (t_{n - 2}), \dots, X (t_{2}) - X (t_{1}), X (t_{1}), \forall t_{1} < t_{2} < \dots < t_{n}$ 相互独立且 $X (t + s) - X (t)$ 分布不依赖于 $t$
标准布朗运动： $σ = 1$
$X (t)$ 是 $t$ 的连续函数但处处不可微

可以证明 $P {lim_{h \to \infty} (X (t + h) - X (t)) = 0} = 1$ 。注意到随机变量 $X (t + h) - X (t)$ 的均值为 0，方差为 $h$ ， $X (t + h) - X (t)$ 在 $h \to 0$ 时趋于 0 ，由此导出连续性

但 $\frac{X (t + h) - X (t)}{h}$ 具有均值 0 方差 $1 / h$ ，因此易看出其不可微

布朗运动是一个连续时间鞅。

通过增量独立性且服从正态易证
$E (B_{t_{1}} | B_{s}, 0 \leq s \leq t) = E (B_{t_{1}} - B_{t} + B_{t} | B_{s}, 0 \leq s \leq t) = E (B_{t_{1}} - B_{t}) + B_{t} = B_{t}$

设 $s < t$ ，则 $B_{t} | B_{s} \sim N (B_{s}, t - s), B_{s} | B_{t} \sim N (\frac{s}{t} B_{t}, \frac{s (t - s)}{t})$
1. 第一个条件概率结论较为直接，这里推导一下第二个结论。根据结论反推知 $E {B_{s} | B_{t}} = s B_{s} / t$
  因此构造 $B_{s} = B_{s} - \frac{s}{t} B_{t} + \frac{s}{t} B_{t}$ 分离常数 $s B_{s} / t$
2. 当 $s < t$ 的时候，有 $B_{s} - s B_{t} / t$ 和 $B_{t}$ 相互独立。
  根据正态性，只需证明不相关即可，
  $C o v (B_{t}, B_{s} - \frac{s}{t} B_{t}) = C o v (B_{t}, B_{s}) - \frac{s}{t} C o v (B_{t}, B_{t}) = s - \frac{s}{t} t = 0$ 易证
3. 利用独立性可得

V a r (B_{s} - \frac{s}{t} B_{t}) = V a r ((1 - \frac{s}{t}) B_{s} - \frac{s}{t} (B_{t} - B_{s})) = (1 - \frac{s}{t})^{2} s + \frac{s^{2}}{t^{2}} (t - s) = \frac{s (t - s)}{t}

多元布朗运动

设 $(B_{t_{1}}, \dots, B_{t_{n}})$ 是多元布朗运动，那么它服从多元正态分布，均值为 0， $C o v (B_{s}, B_{t}) = E (B_{s} B_{t}) = s \land t$ ，概率密度服从

f (x_{1} \dots, x_{n}) = \prod_{k = 1}^{n} \frac{\exp (- \frac{(x_{k} - x_{k - 1})^{2}}{2 (t_{k} - t_{k - 1})})}{\sqrt{2 π (t_{k} - t_{k - 1})}}, x_{0} = t_{0} = 0

这里仅说明推导一下协方差，通过独立性易验证，不妨设 $s < t$ ，则

\begin{aligned} C o v (B_{s}, B_{t}) & = E {B_{s} B_{t}} \\ = E {B_{s} (B_{t} - B_{s} + B_{s})} \\ = E {B_{s}^{2}} + E {B_{s} (B_{t} - B_{s})} \\ = E {B_{s}^{2}} = s \end{aligned}

Brown 运动的鞅性质

几个常见的有关布朗运动的鞅

设 ${B (t)}$ 是Brown运动，则

${B (t)}$ 是鞅；
${B^{2} (t) - t}$ 是鞅
$\forall u \in R, {\exp (u B (t) - \frac{t u^{2}}{2})}$ 是鞅

Proof

${B (t)}$ 是鞅易证， ${B^{2} (t) - t}$ 是鞅可通过下式易证

\begin{aligned} E [B^{2} (t + s) | F_{t}] - (t + s) \\ = B^{2} (t) + 2 E [B (t) [B (t + s) - B (t)] | F_{t}] + E [{[B (t + s) - B (t)]}^{2} | F_{t}] - (t + s) \\ = B^{2} (t) - t \end{aligned}

下证 $\forall u \in R, {\exp (u B (t) - \frac{t u^{2}}{2})}$ 是鞅
由 $B (t) \sim N (0, t)$ 的矩母函数 $E [e^{u B (t)}] = e^{\frac{t}{2} u^{2}} < \infty$ 说明其可积且 $E [e^{u B (t) - \frac{t u^{2}}{2}}] = 1$ ，通过下式两端同乘 $e^{- \frac{s + t}{2} u^{2}}$ 易证

\begin{aligned} E [e^{u B (t + s)} | F_{t}] \\ = E [e^{u B (t) + u [B (t + s) - B (t)]} | F_{t}] \\ = e^{u B (t)} E [e^{u [B (t + s) - B (t)]} | F_{t}] \\ = e^{u B (t)} E [e^{u [B (t + s) - B (t)]}] \\ = e^{u B (t)} e^{\frac{s}{2} u^{2}} \end{aligned}

零点特性

设 $L_{t} = max {s < t : B_{s} = 0}$ ，则 $P (L_{t} < s) = \frac{2}{π} \arcsin (\sqrt{s / t})$
即给定时间 $t$ ，则之前出现零点的最晚的时刻的概率可求（证明详见 PTE E.g. 8.4.2^[1]）

布朗运动的鞅构造

)

If $u (t, x)$ is a polynomial in $t$ and $x$ with

\frac{\partial u}{\partial t} + \frac{1}{2} \frac{\partial^{2} u}{\partial x^{2}} = 0

then $u (t, B_{t})$ is a martingale.

Proof

检查 Brown 运动的转移概率函数 $p_{t} (x, y)$ 满足热方程，即

p_{t} (x, y) = (2 π)^{- 1 / 2} t^{- 1 / 2} \exp (- (y - x)^{2} / 2 t)

{\begin{cases} \frac{\partial p}{\partial t} = - \frac{1}{2} t^{- 1} p_{t} + \frac{(y - x)^{2}}{2 t^{2}} p_{t} \\ \frac{\partial p}{\partial y} = - \frac{y - x}{t} p_{t} \\ \frac{\partial^{2} p}{\partial y^{2}} = - \frac{1}{t} p_{t} + \frac{(y - x)^{2}}{t^{2}} p_{t} \end{cases} ⟹ \frac{\partial p_{t}}{\partial t} = \frac{1}{2} \frac{\partial^{2} p_{t}}{\partial y^{2}}

交换微分与积分，并利用上述热方程可得

\begin{aligned} \frac{\partial}{\partial t} E_{x} u (t, B_{t}) & = \int \frac{\partial}{\partial t} (p_{t} (x, y) u (t, y)) d y \\ = \int [u (t, y) \frac{\partial p_{t}}{\partial t} + p_{t} (x, y) \frac{\partial u}{\partial t}] d y \\ = \int \frac{1}{2} \frac{\partial}{\partial y^{2}} p_{t} (x, y) u (t, y) + p_{t} (x, y) \frac{\partial}{\partial t} u (t, y) d y \\ = \int p_{t} (x, y) (\frac{\partial}{\partial t} + \frac{1}{2} \frac{\partial}{\partial y^{2}}) u (t, y) d y = 0 \end{aligned}

即说明 $E_{x} u (t, B_{t})$ 与时间 $t$ 无关，其无条件期望保持不变
3. 下证 $E [u (t, B_{t}) ∣ F_{s}] = u (s, B_{s})$ 即证鞅的定义
构造辅助函数 $v (r, x) = u (s + r, x)$ ，易知其仍满足热方程。由于 $B_{t} = B_{s} + (B_{t} - B_{s}) \sim B_{s} + B_{t - s}$ （布朗运动增量平稳性）

E [u (t, B_{t}) ∣ F_{s}] = E [v (t - s, B_{t}) ∣ F_{s}] = E [v (t - s, B_{s} + B_{t - s}) | F_{s}] = E_{B_{s}} [v (t - s, B_{t - s})]

其中最后一个等式即 $B_{s}$ 出发的 $B_{t - s}$ 的期望

\begin{aligned} E [v (t - s, B_{s} + B_{t - s}) ∣ F_{s}] & = \int_{- \infty}^{\infty} v (t - s, B_{s} + y) \cdot \frac{1}{\sqrt{2 π (t - s)}} e^{- \frac{y^{2}}{2 (t - s)}} d y \\ = \int_{- \infty}^{\infty} v (t - s, z) \cdot \frac{1}{\sqrt{2 π (t - s)}} e^{- \frac{(z - B_{s})^{2}}{2 (t - s)}} d z \\ = E_{B_{s}} [v (t - s, B_{t - s})] \end{aligned}

由上述第二点证明可知，期望与初始点一致即 $E_{B_{s}} [v (t - s, B_{t - s})] = v (0, B_{s})$ ，综上

E [u (t, B_{t}) ∣ F_{s}] = u (s, B_{s})

即证明为鞅。

离出时间分析

对 Brown 运动，定义 $T_{y} = inf {s > 0 : B_{s} = y}$

设

a < 0 < b

，则

P (T_{a} < T_{b}) = \frac{b}{b - a}, P (T_{a} > T_{b}) = \frac{- a}{b - a}

证明参考【鞅与停时】停时理论#停时定理的应用易证

设

a < 0 < b, τ = inf {t : B_{t} \notin (a, b)}

，则

E (τ) = - a b

证明思路即构造鞅 ${B_{t}^{2} - t}$ ，则依据上述概率有

\begin{aligned} E (B_{τ}^{2} - τ) = 0 \\ ∴ & E (τ) = a^{2} P (T_{a} < T_{b}) + b^{2} P (T_{a} > T_{b}) = - a b \end{aligned}

当 $a \to - \infty$ 时，有 $E (τ) \to \infty$ 说明布朗运动到达任意点的首达时间趋于无穷，实质上为零常返

如果是2维的布朗运动，零常返性还是成立的，但是到3维以上的情况就没有常返性了

（这里给出离散情形下对称随机游走的证明，可直观推广到布朗运动中——下面的求和变积分即可）设 $I_{k}$ 为第 k 步是否回归原点的指示函数，则返回原点次数的期望为 $E {\sum_{k = 0}^{\infty} I_{k}} = \sum_{k = 0}^{\infty} P {I_{k} = 1} = \sum_{k = 0}^{\infty} p_{k}$
由对称性可知 $I_{2 n + 1} = 0$ ，因此 $d$ 维下布朗运动回到原点次数的期望可表示为 $\sum_{n = 1}^{\infty} p_{2 n}^{(d)}$ ，下面即要分析其对不同 d 的敛散性
../../PHOTO/【随机过程】布朗运动/img-20250425201033310.png|400
【 $d = 1$ 】

\begin{aligned} p_{2 n}^{(1)} & = \frac{(2 n)!}{n! n!} \cdot \frac{1}{2^{n}} \\ \sim \frac{\sqrt{4 π n} (2 n / e)^{2 n}}{2 π n (n / 2)^{2 n} 2^{2 n}} (Strling Formula) \\ \sim C n^{- 1 / 2} \end{aligned}

【 $d = 2$ 】

\begin{aligned} p_{2 n}^{(2)} & = \frac{1}{4^{2 n}} \sum_{k = 0}^{n} \frac{(2 n)!}{k! k! (n - k)! (n - k)!} \\ = \frac{1}{4^{2 n}} C_{2 n}^{n} \sum_{k = 0}^{n} (C_{n}^{k})^{2} \\ (*) & = \frac{1}{4^{2 n}} (C_{2 n}^{n})^{2} \\ \sim C n^{- 1} \end{aligned}

由于 $\sum_{n = 1}^{\infty} n^{- 1 / 2}, \sum_{n = 1}^{\infty} n^{- 1}$ 均发散，也即为常返的
【 $d > 2$ 】

\begin{aligned} p_{2 n}^{(d)} & = \frac{1}{(2 d)^{2 n}} \sum_{\sum i_{j} = n} \frac{(2 n)!}{(i_{1}! i_{2}! \dots i_{d}!)^{2}} \\ = C_{2 n}^{n} \frac{1}{(2 d)^{2 n}} \sum_{\sum i_{j} = n} {(\frac{n!}{i_{1}! i_{2}! \dots i_{d}!})}^{2} \\ \leq C_{2 n}^{n} \frac{1}{(2 d)^{2 n}} \frac{(d m)!}{(m!)^{d}} \sum_{\sum i_{j} = n} \frac{n!}{i_{1}! i_{2}! \dots i_{d}!} \\ (**) & = C_{2 n}^{n} \frac{(d m)!}{(2 d)^{2 n} (m!)^{d}} d^{n} \\ \sim C n^{- d / 2} \end{aligned}

$(*)$ 等式利用二项式求和即构造 $(1 + x)^{2 n} = (1 + x)^{n} (1 + x)^{n}$ ，则 $x^{k}$ 系数 $C_{2 n}^{k} = \sum_{i = 0}^{k} C_{n}^{n} C_{n}^{k - i}$ ; $(* *)$ 同理易证
由于 $\sum_{n = 1}^{\infty} n^{- p}, p > 1$ 收敛，因此其非常返

Brown 运动的几种变形

在原点反射的 Brown 运动：令

Y (t) = | B (t) |, t ⩾ 0

定义的过程 ${Y (t), t ⩾ 0}$ 称为在原点反射的 Brown 运动。

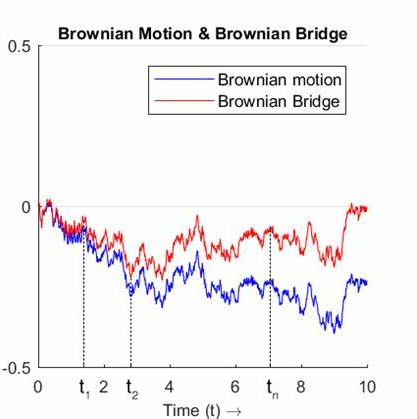
布朗桥

Brownian Bridge

设 ${B (t), t ⩾ 0}$ 是Brown运动，令

B^{*} (t) = B (t) - t B (1), 0 ⩽ t ⩽ 1

称随机过程 ${B^{*} (t), 0 ⩽ t ⩽ 1}$ 是Brown桥。

布朗桥特点： $B^{*} (0) = B^{*} (1) = 0$ ，过程的起点和终点一致（类似桥的形状）

几何Brown运动

X (t) = e^{B (t)}, t ⩾ 0

金融市场中，经常假定股票的价格的变化是几何Brown运动

Probability: Theory and Examples (豆瓣) ↩︎ ↩︎