数据建模

【例】英语中字母组合惠影响后面字母的出现概率

• 基于统计观察的相邻关系，通常称作“预测”编码器，可视为统计压缩的加强版

该书作者在注脚中提到“预测”编码器这一名词可能产生的误解，因为“预测”意味着可能出错，不符合编码直觉认知，因此更难喜欢称其为多上下文算法

• 将自适应模型 与多种码字对应表 结合，根据前面观察到的符号，为当前符号生成尽可能短的码字。

Markov 链

略，详见...

Markov 链与压缩

略，实际没有人真正地使用马尔可夫链来压缩数据，至少不会用书中提到的简单方法来压缩（内存容量与复杂度过高）。

人们创造了各种衍生算法，这些算法所需要的内存要比一般的马尔可夫链算法小，性能也更好一些。其中，最值得关注的是部分匹配预测算法和上下文混合算法，下面来介绍这两种算法。

部分匹配预测算法

部分匹配预测算法（prediction by partial matching，PPM）通过前 $N$ 个符号的上下文来决定第 $N+1$ 个符号最有效的编码方式。
简单马尔可夫链会采用比较直接的实现方式，即读取当前符号并判断它是否是现有链条的延续，PPM 算法的实现恰好相反。给定输入流中的当前符号，PPM 算法会向前扫描 $N$ 个符号，并根据前 $N$ 个符号的上下文来决定当前符号的出现概率。

工作流程

1. 编码器从输入流中读取下一个字符S。
2. 编码器扫描最近读取的 $N$ 个字符，也就是 $N$ 阶的上下文。
3. 根据最近读取的这些字符，编码器确定字符S出现在特定的上文后的概率 $P$。
4. 如果这一概率为 0，编码器就会输出转义标记，这样解码器就能反映这一过程。
5. 然后，编码器继续从第二步的扫描操作开始，只不过扫描的字符个数由 $N$ 变为 $N–1$，直到所得的概率 $P$ 不为 0 或者没有字符可以继续扫描。
6. 如果没有字符可以继续扫描，就为 $P$ 赋上固定的概率值（例如基于字符出现频率的概率值）。
7. 最终编码器通过统计编码的形式以概率 $P$ 编码字符S。

Trie树（前缀树）

PPM 算法需要一种数据结构，可以将从输入流中读取的每个字符的所有上下文（$0\sim N$ 阶）存储起来，并且在需要时能快速定位到。在简单的情况下，可以通过一种被称为单词查找树（trie）的特殊树结构来实现这样的需求，这种树的每个分支都表示一种上下文。

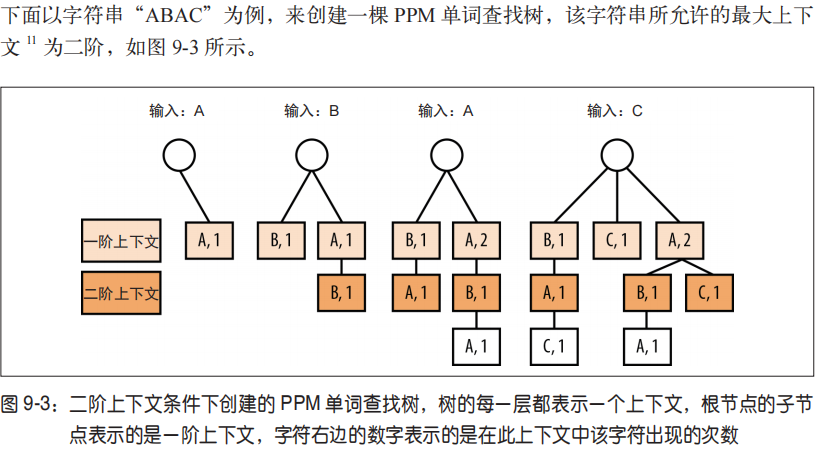
选择一个合理的N值

似乎上下文越长（也就是 $N$ 的取值越大），预测的效果越好。然而，大多数 PPM 算法的实现在综合考虑所需内存、处理速度以及压缩率后，将 $N$ 的值设定为 5 或者 6。

如何处理未知符号

PPM 算法（模型）的大部分优化工作是在处理输入流中那些之前没有出现过的字符。显而易见的处理方法是通过创建“从没见过”的符号来触发转义序列（escape sequence），但
是存在零频问题（zero-frequency problem）：没有见过的符号应该赋什么样的概率值？

有一种 PPM 算法的变体使用拉普拉斯估计（Laplace estimator），赋给所有“从没见过”的符号相同的伪计数值 1。还有一种被称为 PPMD 的变体是这样处理这一问题的，“从没见过”的符号每使用一次，伪计数值就加 1。（换句话说，PPMD 算法是这样估算新出现符号的概率的，即新符号的概率等于不同符号的个数与观察到的所有符号的出现次数之比。）

上下文混合算法

上下文混合算法（context mixing），即为了找出给定符号的最佳编码，我们会使用两个或者更多的统计模型。上下文混合算法也带来了以下两个很有意思的问题：

• 应该使用什么样的模型？
• 应该怎样将这些模型结合起来？

使用什么样的模型？

• 对数据压缩来说，相邻性是一个很重要的课题。LZ、RLE、增量编码以及 BWT 这些算法都是基于这样的假设：数据的相邻性与它的最佳编码方式有关。但相邻性和局部性都只是上下文的最简单形式，而绝不是唯一的形式。
• 我们所说的模型其实就是用来识别和描述符号之间的关系。通过对数据的建模，我们就能对数据中包含的各种属性了解得更多，因而也就越能描述好当前的符号。
• PAQ，上下文混合算法的先驱压缩器之一，包含以下模型
  • n 元语法（n-grams），这里上下文是指在被预测符号之前的 n 个字符（与 PPM 算法相同）
  • 整词 n 元语法（whole-word n-grams），忽略大小写和非字母字符（对文本文件很有用）
  • “稀疏”上下文，例如，被预测符号之前的第二个和第四个字节（对某些二进制文件很有用）
  • “模拟”上下文，由前面的 8 位或者 16 位字节的高字节位组成（对多媒体文件很有用）
  • 二维上下文（对图像、表和电子表格很有用），行的长度由找出的重复字节模式的步长决定
  • 只针对特定文件类型的特殊模型，例如 x86 可执行文件，BMP、 TIFF 或者 JPEG 格式的图片

怎样混合这些模型？

• 线性混合（linear mixing）
  • 将各个模型的预测值加权平均的过程，最终的值则取决于证据权重
  • 缺点：没有反馈回路来说明在预测如何压缩数据时赋给一个模型的权重是否正确。因此，当输入数据流变化时，难以保证效果
• 逻辑混合
  • 使用了神经网络来更新权重，而更新的依据则是哪个模型在过去给出了最准确的预测
  • 在进行数据压缩时，它需要消耗大量的内存，同时运行的时间也较长（如果看一些在 LTCB 上运行的 ZPAQ，你会发现压缩 1 G 的文件需要 14 G 的内存。这些压缩的中间数据都需要空间去存储。）

© 2024 LiQ :) 由 Obsidian&Github 强力驱动