本节定义熵|相对熵|互信息等度量以及常用不等式,这些度量作为后续通信、统计、复杂性和赌博中许多问题的自然答案而出现,也是这些定义的价值所在。
主要内容
- Properties of
- Conditioning reduces entropy(条件熵性质),当 时等号成立
- , 当且仅当 相互独立时取等
- , 当且仅当 服从 上的均匀分布等号成立。
- is concave in .
- Relative Enrtopy
-
相对熵 与互信息 性质
- 当且仅当 时等号成立
- 若 且 是 上的均匀分布,则
- 关于 时凸的
-
链式法则
-
Jensen 不等式
-
对数和不等式
-
充分统计量: is sufficient relative to if and only if for all distributions on .
-
Fano 不等式:
-
若 独立同分布,则
熵 (Entropy)
The entropy of a discrete random variable is
- 是 的期望
- 熵度量了随机变量的“随机性”
- 熵的对数 log 所用底为 2,单位为 bit。若使用底为 时单位为 nat(奈特)。
- 上的均匀分布是其最大熵分布
证明利用定义的相对熵
其中 是均匀分布概率质量函数
对一个服从二项分布的随机变量 有
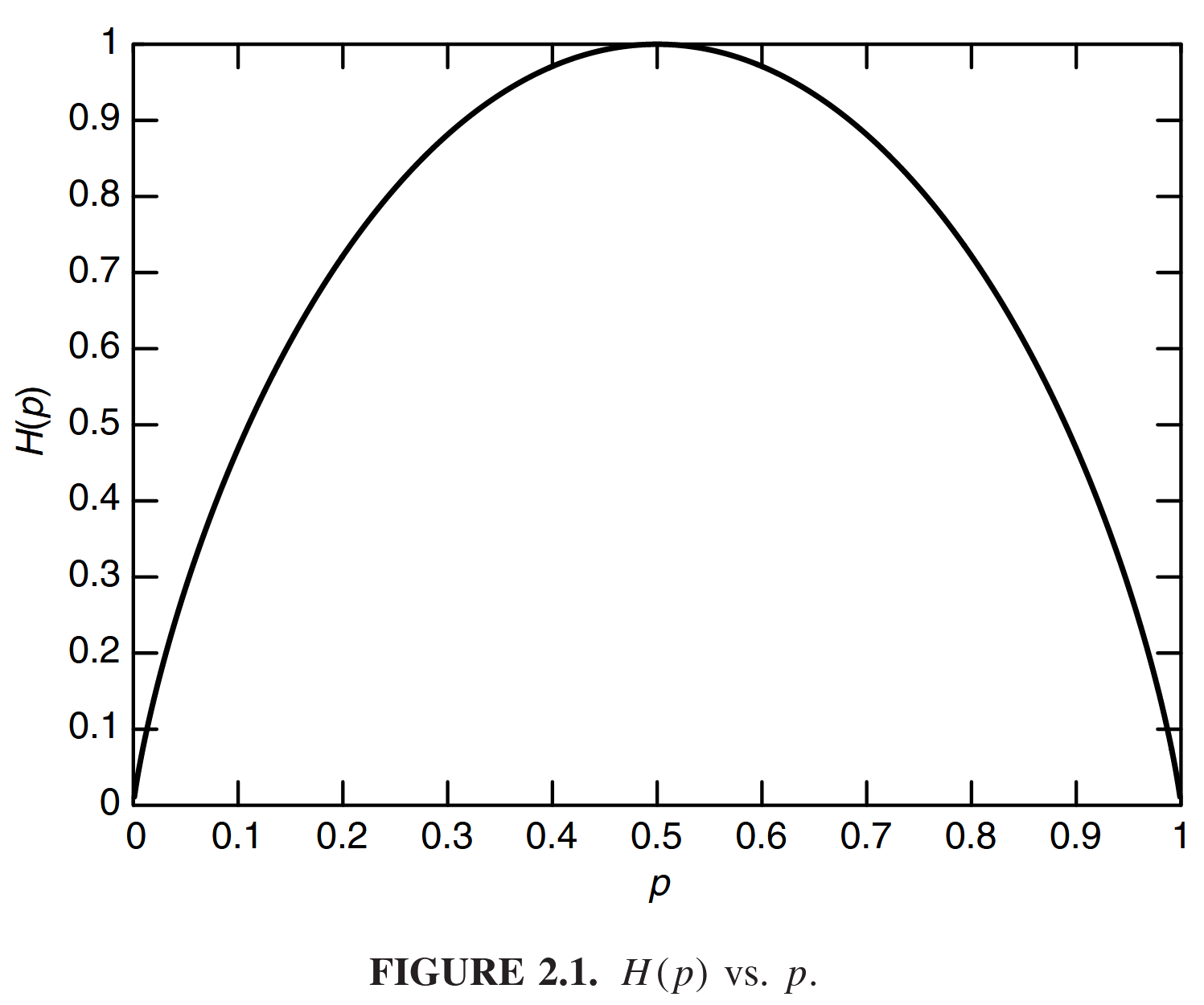
可以看出 是凹函数。
Joint Entropy & Conditional Entropy
The joint entropy of a pair of discrete random variables with a joint distribution is defined as
the conditional entropy is defined as
- 联合熵可表示为 ; 条件熵可表示为
相对熵 (Relative Enrtopy)
相对熵是两个随机分布之间距离的度量。统计学中对应似然比的对数期望。
若已知随机变量真实分布为
, 但却使用针对分布
的编码,那么平均需要
比特描述该随机变量。
利用 Jensen's inequality (2.85) 进行证明。设 为 支撑集,则
利用 Log sum inequality 证明:
- 相对熵不对称,也不满足三角不等式,因此实际上并非两个分布之间的真实距离
- 相对熵的凸性: 关于 是凸的
同理利用对数和不等式易证。
互信息是一个随机变量包含另一个随机变量信息量的度量。也即给定另一随机变量“知识”的条件下,原信息量不确定性的缩减量。
上式为离散型随机变量情形,微分熵中奖探讨含有连续随机变量的情形。
证明利用
【条件互信息(conditional mutual information)】
Chain Rules
证明主要利用定义以及 直接推导 (2.15~2.19)
- 【推论】
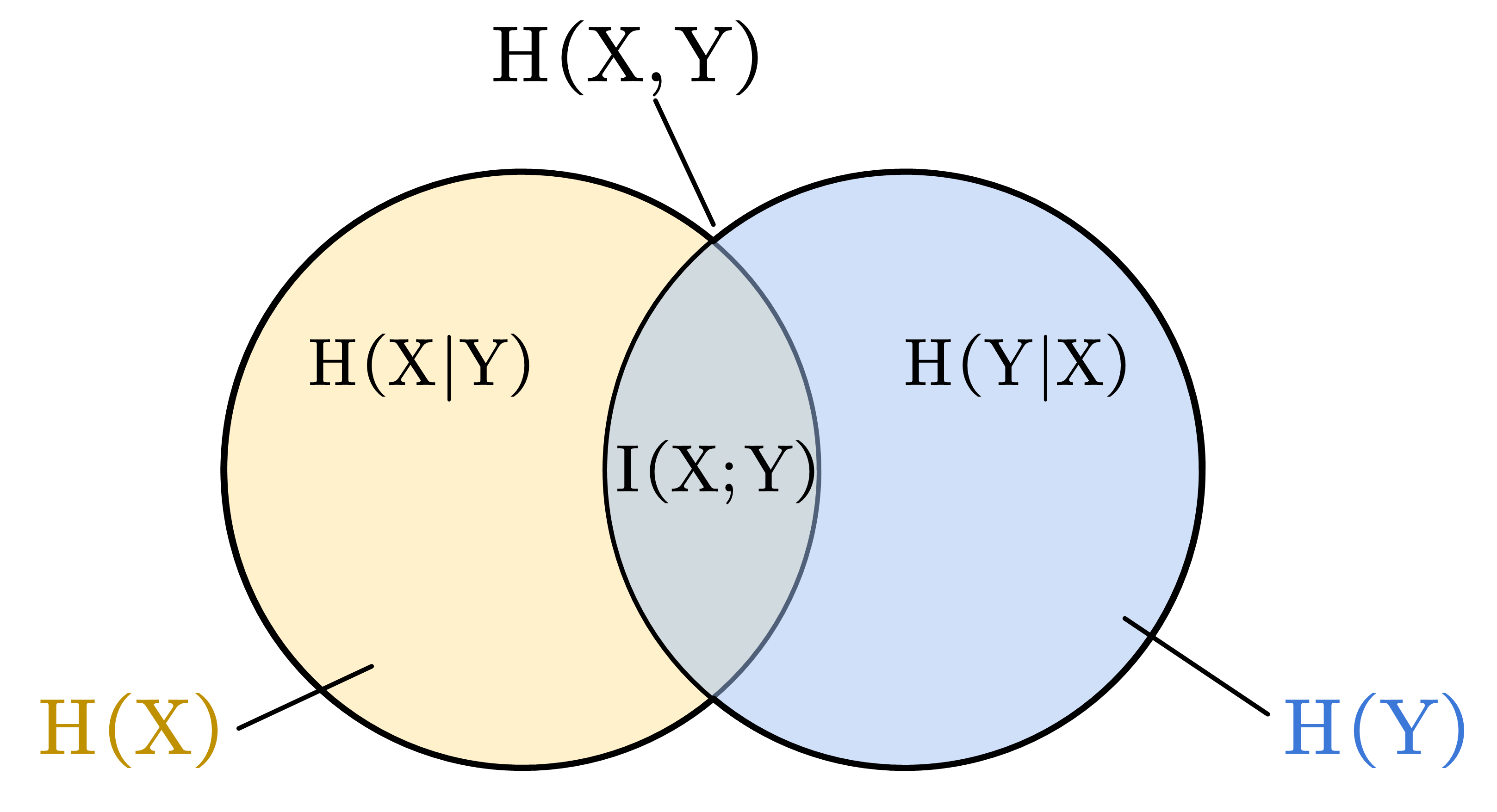
注意
- Mutual information & entropy
证明利用 与定义递推
- Chain rule for information
利用 以及上述熵的链式法则易证
- Chain rule for relative entropy
其中条件相对熵 是在 上对 之间相对熵的平均值。
证明思路利用 进行 log 的拆分易证(2.68~2.71)
- Independence bound on entropy
根据上述图例以及定义易证,且当 相互独立时取等。
常用不等式
Jensen's inequality
If is a convex function and is a random variable,
Moreover, if is strictly convex, the equality implies that i.e., is a constant.
- 如果是 concave 则变为 。
离散情形下可利用数学归纳法(两点分布利用凸函数定义直接得到)
Log sum inequality
(对数和不等式)对于非负数
当且仅当 时等号成立。
【证明思路】
不等式等价于
利用 Jensen's inequality,因为 严格凸; LHS 即 ,RHS 即 得证。
Data-processing inequality
If X → Y → Z forms a Markov chain,
Fano's inequality
其他
- If and are i.i.d. with entropy ,
with equality if and only if has a uniform distribution.
© 2024 LiQ :)
由 Obsidian&Github 强力驱动


