型方法与大偏差理论

#信息论 #统计

大偏差理论关注概率分布序列的远端尾部的渐近行为，即关注与期望偏差较大，稀有事件的概率。更进一步，该理论关注某些极端事件或尾部事件的概率度量的指数下降。而型方法是研究该问题的强有力工具，Cover 书^[1] 中型方法用于计算稀有事件概率，通用信源编码存在性证明，以及假设检验中的应用。

Notations & Definitions

这里 Notation 定义参考文献 2^[2]，不影响理解

$A$ : alphabet，一个字母表
$A^{n} = {x^{n}}$ : 符号序列 $x^{n}$ 组成的集合

$x^{n}$ 可简记 $x$

$A^{\infty}$ : infinite sequences set
$A^{*}$ : all finite sequences set，include $\emptyset$

型(type) | 型类(type class)

型：样本数为 $n$ 的经验概率分布 $P_{x^{n}} (a) = \frac{| {i : x_{i} = a} |}{n} = \frac{N (a | x^{n})}{n}, a \in A, x^{n} \in A^{n}$

记 $P_{n} = {P_{x^{n}}}$

型类：序列长度为 $n$ 且型为 $P$ 的序列全体 $T^{n} (P) = {x^{n} \in A^{n} : P_{x^{n}} = P}$

如 $A = {0, 1}$ ，则型的集合为 $P_{n} = {(\frac{0}{n}, \frac{n}{n}), (\frac{1}{n}, \frac{n - 1}{n}) \dots, (\frac{n}{n}, \frac{0}{n})}$ ，中每个元素为一种型

型的性质

为便于表示，上标 n 有时省略

P_{n}

大小

$| P_{n} | = C_{n + | A | - 1}^{| A | - 1} \leq (n + 1)^{| A |}$

采样结果出现在某一型类概率

若采样独立同分布，服从 $P (x)$ (distribution $P$ on $A$ )，则 $x^{n}$ 出现概率仅依赖于其型

P^{n} (x) = 2^{- n (H (Q) + D (Q ∥ P))}

同为上述例子 $A = {0, 1}$ ，直观易知出现 010101 与 000111 概率其实一致，只与出现几个 1，几个 0 有关

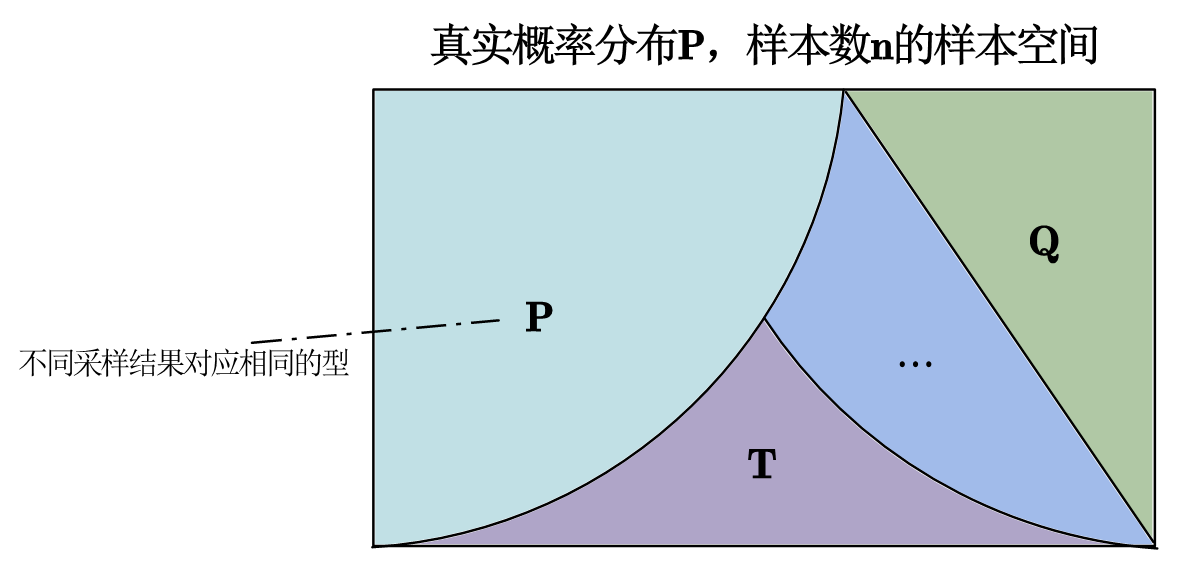
可以看出，上述定理表明，对于i.i.d.的采样，采样结果可以按照型类来划分，且同一型类下所有采样序列出现的概率一致，与 AEP 有类似之处。

型类大小

$\frac{1}{| P_{n} |} 2^{n H (P)} \leq | T (P) | \leq 2^{n H (P)}$

某一型类出现概率

$\frac{1}{| P_{n} |} 2^{- n D (Q ∥ P)} \leq P^{n} (T (Q)) \leq 2^{- n D (Q ∥ P)}$

Proof

对于 $P_{n}$ 的大小，即 n-type 的种类个数，等价于将 n 个相同的球放入 $| A |$ 个不同盒子最终有几种情况的排列组合问题。由于允许盒子内放 0 个球，因此利用添元素隔板法，即结果为 $C_{n + | A | - 1}^{| A | - 1}$
设采样得到的型为 $Q (x^{n})$ ，则出现 $x_{i}$ 的次数为 $n Q (x_{i})$ ；易求

P (x) = \prod_{a \in A} P (a)^{n Q (a)} = 2^{n \sum_{a \in A} Q (a) \log P (a)} = 2^{n (- H (Q) - D (Q ∥ P))}

RHS：当 $P = Q$ 时，通过 2 知， $T (P)$ 内每个序列概率均为 $2^{- n H (P)}$ ；又整个型类出现概率小于 1，即 $2^{- n H (P)} \cdot | T (P) | \leq 1$ ；
LHS：当 $P = Q$ 时，直观理解出现型类 $T (P)$ 概率在所有型类中理应最大。因此 $1 \leq | P_{n} | max_{P} P r (T^{n} (P)) = | P_{n} | \cdot P r (T^{n} (P)) = | P_{n} | \cdot 2^{- n H (P)} \cdot | T^{n} (P) | ◻$
上述结果 2 与 3 的不等式相乘即证

下述定理给出型类陈述的（弱）大数定律。上述定理可知，型的最重要性质为：型的数量为多项式级，而序列数量为指数级，由于每个型类概率以指数依赖于真实分布与型之间的相对熵，因此对于原理真实分布的型类概率依指数衰减。

弱大数定律

设 $X_{1}, X_{2}, \dots, X_{n} \sim p (x)$ 为 i.i.d，则

P r (D (\hat{P_{n}} ∥ P_{n}) \geq δ) \leq | P_{n} | 2^{- n δ}

进一步可知， $D (\hat{P_{n}} ∥ P_{n}) \to 0$ 依概率 1 成立

也可用于证明 AEP^[1:1]

Proof

|450
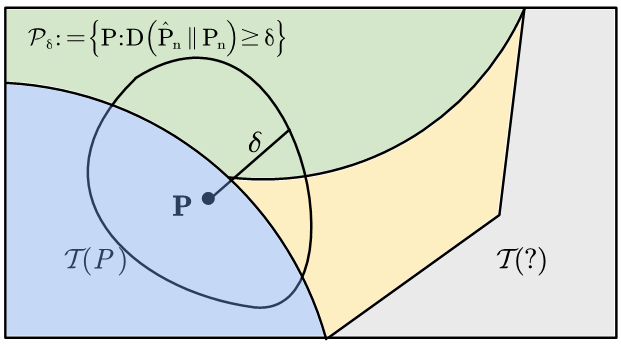
易知 $| P_{δ} | \leq | P_{n} |, 2^{- n min D (\hat{P} ∥ P)} \leq 2^{- n δ}$

L H S \leq \sum_{T_{Q} \in P_{δ}} P r (T_{Q}) \leq | P_{δ} | \cdot 2^{- n min D (\hat{P} ∥ P)} \leq | P_{n} | \cdot 2^{- n δ}

Sanov 定理

假设南京梅雨季节天气情况为 $X$ ， $P r {X = 晴天} = P r {X = 雨天} = \frac{1}{2}$ ，且独立同分布，则采样一段天数 ( $n$ 天) 中雨天天数不少于 $\frac{7}{10} n$ 的概率？

不妨假设晴天/雨天对应 $X_{i} = 1 / 0$ ，由中心极限定理可知 $\frac{1}{n} \sum_{i = 1}^{n} X_{i} \to \frac{1}{2}$
而所求概率为 $P {\frac{1}{n} \sum_{i = 1}^{n} X_{i} \geq \frac{7}{10}}$ ，相比期望是一个比较大的偏差，虽然可以通过 Bernoulli 分布计算出精确概率值（且 n 较大时计算量极大），但大偏差理论更关心这一概率随 n 变化的衰减速度。（更精确地，稀有事件发生概率一般写作 $P [∣ {\overset{―}{S}}_{n} - p ∣\geq a] = C_{n} e^{- γ n}$ ，相比修正项 $C_{n}$ ，更关注主要指数项 $γ$ ）

针对偏差与概率间关系的常用公式
- Chebyshev (切比雪夫) 不等式
$P {| X - E (X) | \geq ϵ} \leq \frac{D (X)}{ϵ^{2}}$
- CLT (中心极限定理)
$P {| \overset{―}{X} - E (X) | \leq ϵ} ⟶ Φ (\frac{ϵ \sqrt{n}}{σ})$

然而 Chebyshev 不等式只适用于单变量，CLT 以 $\sqrt{n}$ 指数衰减。实现在一个合理的相对误差边界内做估计就需要一个大的样本容量 (即 n)，因此希望改善截尾概率的估计。

Sanov（萨诺夫）定理

设 $E \subseteq P_{n}$ 为全体概率分布的子集， $Q$ 为以概率分布。定义 $D (E ∥ Q) = min_{P \in E} {D (P ∥ Q)} = D (P^{*} ∥ Q)$ ，若集合 $E$ 为闭包（保证 $P^{*} \in E$ ），则

- \frac{1}{n} \log Q^{n} (E) \to D (P^{*} ∥ Q)

证明思路

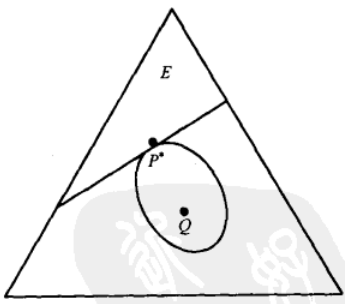
上界：由于 $P r (x^{n}) = 2^{- D (P ∥ Q)} \leq 2^{- D (P^{*} ∥ Q)}$

Q^{n} (E) \leq | E | \cdot 2^{- D (P^{*} ∥ Q)} \leq | P_{n} | \cdot 2^{- D (P^{*} ∥ Q)}

下界：由于 $P^{*} \in E$ ，因此

Q^{n} (E) \geq P r (T_{P^{*}}^{n}) \geq | P_{n} |^{- 1} \cdot 2^{- n D (P^{*} ∥ Q)}

上述为证明方便， $P^{*} \in E$ ，但实际上 n 有限时 $P^{*}$ 不一定在 $E$ 内，不过可以证明可找到一列分布 $P_{n}$ ，使得 $P_{n} \in E$ 且 $D (P_{n} ∥ Q) \to D (P^{*} ∥ Q)$ 由此易证

续上面的例子，可对应概率分布集合 $E = {(p, 1 - p) | p \geq 7 / 10}$ ，真实分布 $Q = (1 / 2, 1 / 2)$ ，可得 $P^{*} = (7 / 10, 3 / 10)$ 。因此可估计 $P {\frac{1}{n} \sum_{i = 1}^{n} X_{i} \geq \frac{7}{10}} ≐ 2^{- n D (P^{*} ∥ Q)} = 2^{- 0.119 n}$

Draft

参考资料

《信息论基础》Thomas M. Cover 第 11 章信息论与统计学 ↩︎ ↩︎
Information Theory and Statistics: A Tutorial Chapter 2 ↩︎