【Stats300A】L2

指数族

指数族可以描述许多常见分布（正态分布，二项分布，泊松分布等），且其与 sufficiency 以及最优 data reduction 密切相关

exponential family

The model ${P_{θ} : θ \in Ω}$ forms an s-demensional exponential family if each $P_{θ}$ has density of the form:

p (x; θ) = \exp (\sum_{i = 1}^{s} η_{i} (θ) T_{i} (x) - B (θ)) h (x)

$η_{i} (θ) \in R$ are called the natural parameters
$T_{i} (x) \in R$ are its sufficient statistics
$B (θ)$ is the log-partition function (logarithm of a normalization factor)

B (θ) = \log (\int \exp (\sum_{i = 1}^{s} η_{i} (θ) T_{i} (x)) h (x) d μ (x)) \in R

$h (x) \in R$ is base measure

$h (x)$ 是一个与参数无关的基准测度，can be “absorbed” into the measure $μ$

【例】指数分布

$P = {Exp (θ) : θ > 0}$ 对应概率密度：

p (x; θ) = θ e^{- θ x} I [x \geq 0] = \exp (- θ x + \log (θ)) I [x \geq 0]

一维指数族：

$η (θ) = - θ$
$T (x) = x$
$B (θ) = - \log (θ)$
$h (x) = I [x \geq 0]$

$η (θ), T (x)$ 中对应的符号可以给两者任意一个。因此指数族的参数化不是唯一的

【例】Beta 分布

$P = {Beta (α, β) : α, β > 0}, θ = (α, β)$ 对应概率密度：

\begin{aligned} p (x; θ) & = x^{α - 1} (1 - x)^{β - 1} I [x \in (0, 1)] \frac{Γ (α + β)}{Γ (α) Γ (β)} \\ = \exp ((α - 1) \log (x) + (β - 1) \log (1 - x) + \log (\frac{Γ (α + β)}{Γ (α) Γ (β)})) I [x \in (0, 1)] \end{aligned}

$η_{1} (θ) = α - 1, η_{2} (θ) = β - 1$
$T = (T_{1}, T_{2})$ for $T_{1} (x) = \log (x), T_{2} (x) = \log (1 - x)$
$B (θ) = - \log (\frac{Γ (α + β)}{Γ (α) Γ (β)})$
$h (x) = I [x \in (0, 1)]$

可以看出一般情况下，几个统计量 $T (x)$ 解决几个“未知参数” $η$

在指数族的定义中，很自然地可以把 $η (θ)$ 当成新的参数 $η$ 来确定密度函数，这样密度函数的主体就是未知参数 $η, T (x)$ 的线性组合，由此引入指数族的自然形式（也称规范形式）：

canonical exponential family

An exponential family is in canonical form when the density has the form

p (x; η) = \exp (\sum_{i = 1}^{s} η_{i} T_{i} (x) - A (η)) h (x)

The natural parameters is $η$ instead of $θ$ .

【例】Gaussian 分布

概率密度：

\begin{aligned} p (x ∣ μ, σ^{2}) & = \frac{1}{\sqrt{2 π} σ} \exp {- \frac{1}{2 σ^{2}} (x - μ)^{2}} \\ = \frac{1}{\sqrt{2 π}} \exp {\frac{μ}{σ^{2}} x - \frac{1}{2 σ^{2}} x^{2} - \frac{1}{2 σ^{2}} μ^{2} - \log σ} \end{aligned}

$η_{1} = μ / σ^{2}, η_{2} = - 1 / 2 σ^{2}$
$T_{1} (x) = x, T_{2} (x) = x^{2}$
$A (η) = \frac{μ^{2}}{2 σ^{2}} + \log σ = - \frac{η_{1}^{2}}{4 η_{2}} - \frac{1}{2} \log (- 2 η_{2})$
$h (x) = \frac{1}{\sqrt{2 π}}$

将可以产生有效的概率密度的 $η$ 集合定义为自然参数空间：

natural parameter space

For each $η \in Θ$ , there exists a normalizing constant $A (η)$ such that $\int p (x, η) = 1$ . Equivalently,

Θ = {η : 0 < \int \exp (\sum_{i = 1}^{s} η_{i} T_{i} (x)) h (x) d μ (x) < \infty}

任意自然形式指数族可写作 $P = {P_{η} : η \in H}$ 且 $H \subseteq Θ$

可证，自然参数空间 $Θ$ 为凸集

指数族的秩

identifiable

$θ$ is identifiable if

θ_{1} \neq θ_{2} \Rightarrow P_{θ_{1}} \neq P_{θ_{2}}

有两种情况可以 reducing the dimension of an s-dimensional exponential family

$\forall x \in X$ ， $T_{i} (x)$ 满足仿射等式约束

Example

$X \sim Exp (η_{1}, η_{2}), p (x; η_{1}, η_{2}) = \exp (- η_{1} x - η_{2} x + \log (η_{1} + η_{2})) I [x \geq 0]$
这里 $T_{1} (x) = T_{2} (x)$ 线性相关。 $(η_{1}, η_{2}) \to η_{1} + η_{2}$ 可实现降维

由于 $p (x; η_{1} + a, η_{2} - a) = p (x; η_{1}, η_{2})$ for any $a < η_{2}$ ，因此非 identifiable

对所有 $η \in H$ ， $η_{i}$ 满足仿射等式约束

Example

$\begin{aligned} p (x; η) & \propto \exp (η_{1} x + η_{2} x^{2}) for all (η_{1}, η_{2}) satisfying η_{1} + η_{2} = 1 \\ = \exp (η_{1} (x - x^{2}) + x^{2}) \end{aligned}$

minimal

A canonical exponential family $P = {P_{η} : η \in H}$ is minimal if

$\sum_{i = 1}^{s} λ_{i} T_{i} (x) = λ_{0}, \forall x \in X \Rightarrow λ_{i} = 0, \forall i \in {0, \dots, s}$ (no affine $T_{i}$ equality constraints)
$\sum_{i = 1}^{s} λ_{i} η_{i} = λ_{0}, \forall η \in H \Rightarrow λ_{i} = 0, \forall i \in {0, \dots, s}$ (no affine $η_{i}$ equality constraints)

full-rank & curved

设 $P = {P_{η} : η \in H}$ 是 s-dimensional minimal exponential family， $T (x) = (T_{1} (x), \dots, T_{s} (x))$ 线性无关，则 $P$ 称作 full-rank exponential family，秩为 $s$
否则称 $P$ 为 curved exponential family

因此可以将指数族分为 3 类：

Non-minimal (有线性关系，可降维)
【例】正态分布 $N (μ, σ^{2})$ , when $μ = σ^{2}, η_{1} = 1 / 2 σ^{2}, η_{2} = 1$
Minimal & Curved (曲线指数族)
【例】正态分布 $N (μ, σ^{2})$ ; $μ = \sqrt{σ^{2}}, η_{1} = 1 / 2 σ^{2}, η_{2} = 1 / \sqrt{σ^{2}} = \sqrt{2 η_{1}}$
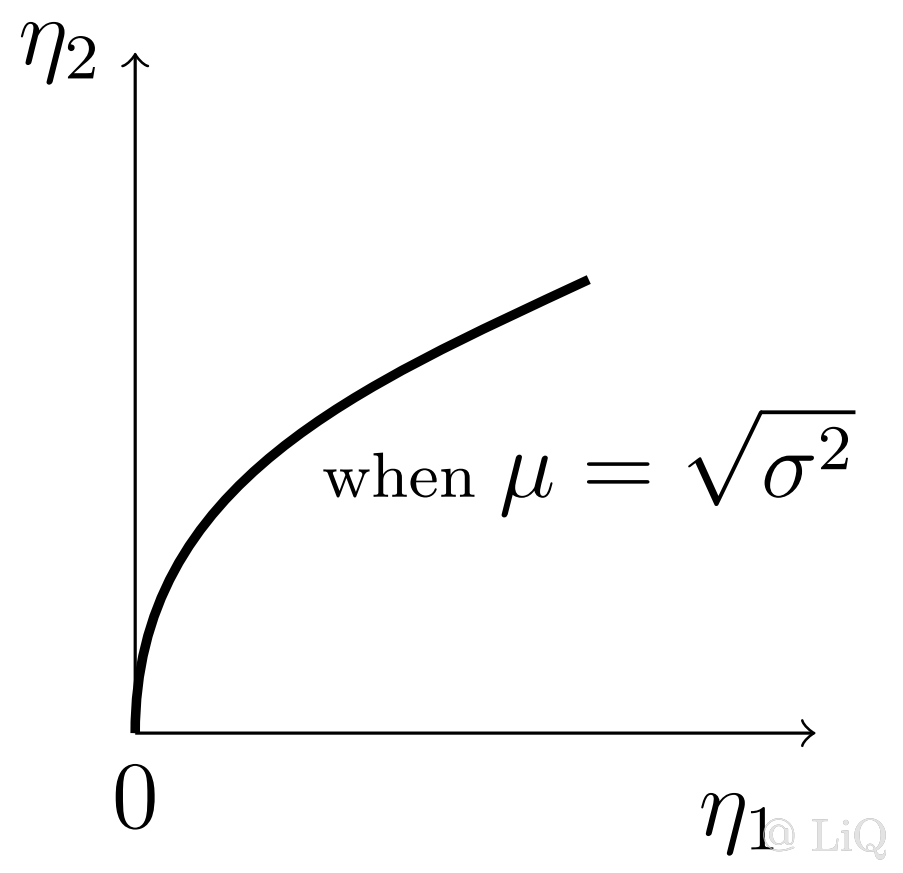
Minimal & Full-Rank (自然参数空间 $= (0, + \infty) \times R$ )

指数族性质

如果 $X_{1}, \dots, X_{n} \overset{iid}{\sim} p (x; θ) = \exp (\sum_{i = 1}^{s} η_{i} (θ) T_{i} (x) - B (θ)) h (x)$ ，则

p (x_{1}, . . ., x_{n}; θ) = \exp (\sum_{i = 1}^{s} η_{i} (θ) \sum_{j = 1}^{n} T_{i} (x_{j}) - n B (θ)) \prod_{j = 1}^{n} h (x_{j})

指数相乘易证； $(\sum_{j} T_{1} (x_{j}), . . ., \sum_{j} T_{s} (x_{j}))$ 是充分统计量

（解析性）设 $f (x)$ 可积， $η \in Θ$ ，则

G (f, η) = \int f (x) \exp {\sum_{i = 1}^{s} η_{i} T_{i} (x)} h (x) d μ (x)

在 $Θ$ 上解析（无穷次可微），且积分微分运算可调换

证明利用 Laplace 变换解析性质

Example

可通过取 $A (η)$ 的偏导数来计算充分统计量的平均值
取 $f (x) = 1$ ，则

\begin{matrix} G (f, η) ≜ \int \exp (\sum_{j = 1}^{s} η_{j} T_{j} (x)) h (x) d μ (x) = \exp (A (η)) \\ \begin{array}{r} \frac{\partial G (f, η)}{\partial η_{i}} = \int T_{i} (x) \exp (\sum_{j = 1}^{s} η_{j} T_{j} (x)) h (x) d μ (x) = \frac{\partial A (η)}{\partial η_{i}} \exp (A (η)) \end{array} \\ \frac{\partial A (η)}{\partial η_{i}} = \int T_{i} (x) \exp (\sum_{i = 1}^{s} η_{j} T_{j} (x) - A (η)) h (x) d μ (x) = E_{η} [T_{i} (x)] \end{matrix}

同理可求任意阶矩如

\frac{\partial^{2} A (η)}{\partial η_{i} \partial η_{j}} = {Cov}_{η} (T_{i} (x), T_{j} (x))

参考

【高等统计学】1. 指数族 - 知乎