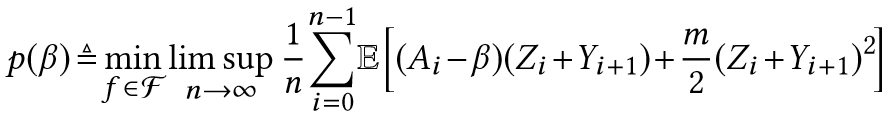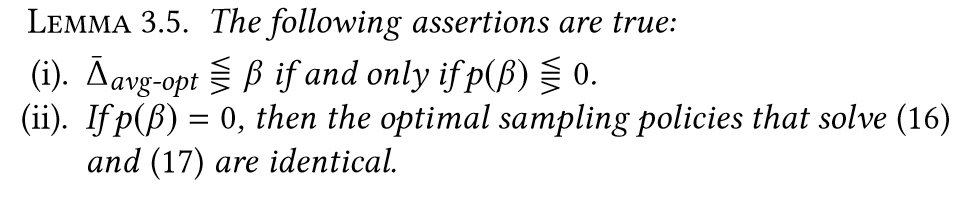Age-optimal Sampling and Transmission Scheduling in Multi-Source Systems

论文链接:Age-optimal Sampling and Transmission Scheduling in Multi-Source Systems

Abstract

In this paper, we consider the problem of minimizing the age of information in a multi-source system, where samples are taken from multiple sources and sent to a destination via a channel with random delay. Due to interference, only one source can be scheduled at a time. We consider the problem of ﬁnding a decision policy that determines the sampling times and transmission order of the sources for minimizing the total average peak age (TaPA) and the total average age (TaA) of the sources. Our investigation of this problem results in an important separation principle: The optimal scheduling strategy and the optimal sampling strategy are independent of each other. In particular, we prove that, for any given sampling strategy, the Maximum Age First (MAF) scheduling strategy provides the best age performance among all scheduling strategies. This transforms our overall optimization problem into an optimal sampling problem, given that the decision policy follows the MAF scheduling strategy. While the zero-wait sampling strategy (in which a sample is generated once the channel becomes idle) is shown to be optimal for minimizing the TaPA, it does not always minimize the TaA. We use Dynamic Programming (DP) to investigate the optimal sampling problem for minimizing the TaA. Finally, we provide an approximate analysis of Bellman’s equation to approximate the TaA-optimal sampling strategy by a water-ﬁlling solution which is shown to be very close to optimal through numerical evaluations.

Main

主要贡献

We prove that, for any givensampling strategy, the Maximum Age First (MAF) scheduling strategy provides the best age performance among all scheduling strategies.
While the zero-wait sampling strategy (in which a sample is generated once the channel becomes idle) is shown to be optimal for minimizing the TaPA, it does not always minimize the TaA.
We provide an approximate analysis of Bellman’s equation to approximate the TaA-optimal sampling strategy by a water-filling solution.
考虑了最小化 AOI 与 peak AOI 两种优化问题
对于 scheduling，总是 MAF 最优（优先发送 age 最大的）；对于 sampling，最小 peak AOI 时零等待采样最优，但对于最小化 average AOI 并非如此，并给出证明

什么模型下 MAF 不是最优的呢??

对于 sampling，利用 lagrange 乘子法得出结论——>threshold policy；再建模为 MDP，利用 DP，Bellman 方程等求解

模型与求解

Because of the randomness of the trans-mission times, our model belongs to the class of semi-Markov de-cision problems (SMDPs)

System Model

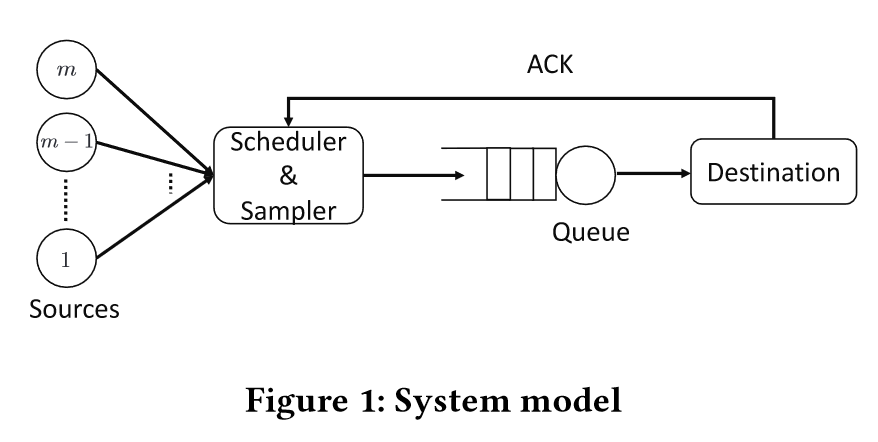
First-Come First Served (FCFS) queue with random i.i.d. service time $Y_{i}$
no buffer (there is no need to generate an update packet during the busy periods.)
$D_{i}$ : delivery time of packet $i$
$Z_{i}$ : waiting time
$U_{l}$ : the most recently delivered packet from source $l$

\begin{array}{r} D_{i} = S_{i} + Y_{i} \\ S_{i + 1} = D_{i} + Z_{i} \end{array}

Age of Information

Δ_{l} (t) = t - U_{l} (t)

Decision policy $d = (π, f)$
implies that a decision policy $d$ follows the scheduling strategy $π$ and the sampling strategy $f$ . $π ≜ (r_{1}, r_{2}, \dots)$ :served source at each transmission opportunity, $f ≜ (Z_{0}, Z_{1}, \dots)$ : sequence of waiting times.

Optimization Problem

\begin{aligned} Δ_{peak} (π, f) & = lim_{n \to \infty} sup_{n \to \infty} \frac{1}{n} E [\sum_{i = 1}^{n} Δ_{r_{i}} (D_{i}^{-})] \\ Δ_{avg} (π, f) & = lim_{n \to \infty} sup_{n \to \infty} \frac{E [\sum_{l = 1}^{m} \int_{0}^{D_{n}} Δ_{l} (t) d t]}{E [D_{n}]} \end{aligned}

Optimal Scheduling Strategy

MAF (Maximum Age First scheduling strategy)

Def 3.1. MAF

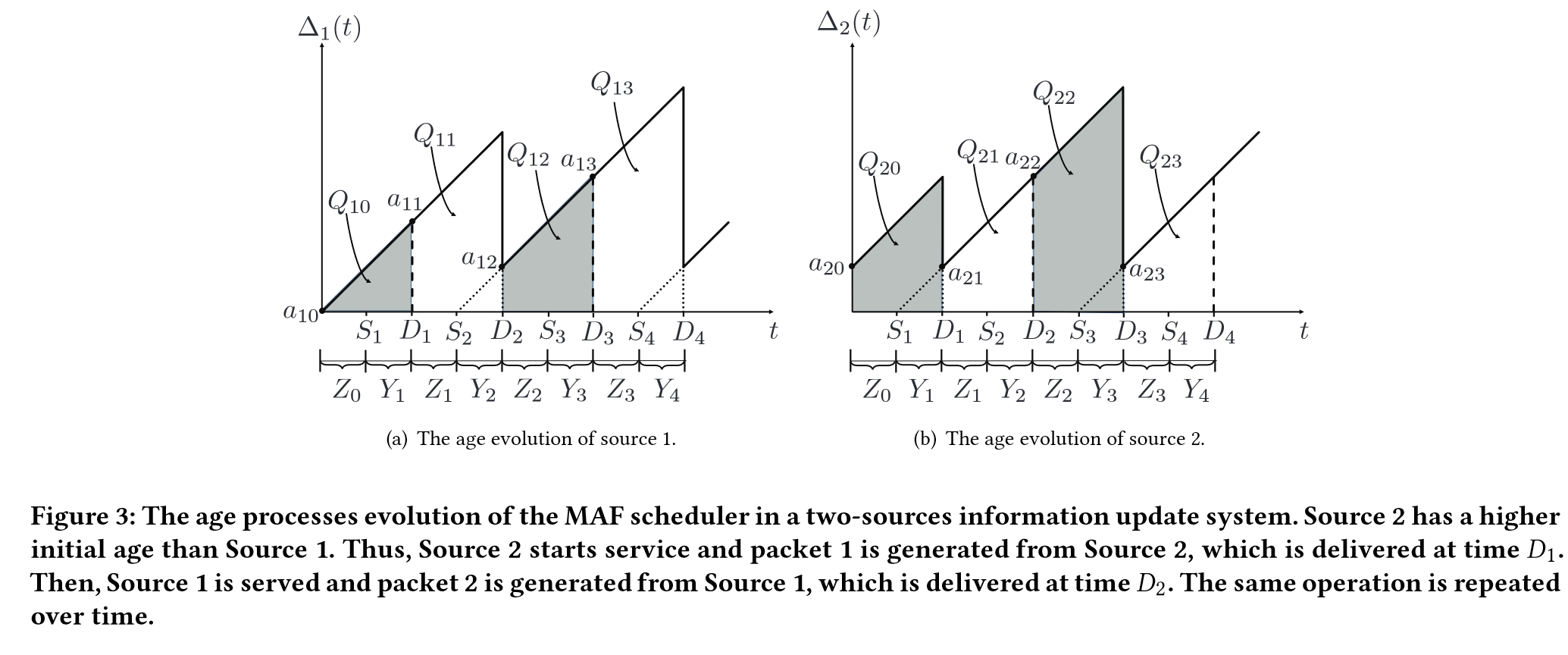
Maximum Age First scheduling strategy: In this scheduling strategy, the source with the maximum age is served the first among all sources. Ties are broken arbitrarily.

PROPOSITION 3.2.
For any given sampling strategy $f \in F, t h e$ MAF scheduling strategy minimizes the TaPA and the TaA, respectively, among all scheduling strategies in $Π$ , i.e. , $\forall f \in F$ and $π \in Π$ ,

Δ_{p e a k} (π_{M A F}, f) \leq Δ_{p e a k} (π, f), Δ_{a v g} (π_{M A F}, f) \leq Δ_{a v g} (π, f) .

证明思路
对于任意采样策略，对所有策略固定其传输时间，只关注发送对象，对于非 MAF 策略，which is not necessary the one with maximum age, and the chosen source becomes the one with minimum age among the m sources after the delivery. 易证

\begin{aligned} {\bar{Δ}}_{peak - opt} & ≜ min_{f \in F} Δ_{peak} (π_{MAF}, f) \\ {\bar{Δ}}_{avg - opt} & ≜ min_{f \in F} Δ_{avg} (π_{MAF}, f) \end{aligned}

Optimal Sampler

Proposition 3.3.
The optimal sampler for minimizing the TaPA is the zero-wait sampler, i.e., $Z_{i} = 0$ for all $i$ .
对于最小化 TaA，Zero-wait 并非最好策略，because the latter metric may not be a non-decreasing function of the waiting times

\begin{aligned} \int_{0}^{D_{n}} Δ_{l} (t) d t & = \sum_{i = 0}^{n - 1} Q_{l i} \\ Q_{l i} & = a_{l i} (Z_{i} + Y_{i + 1}) + \frac{1}{2} (Z_{i} + Y_{i + 1})^{2} \end{aligned}

\begin{matrix} (16) & \begin{array}{r} {\bar{Δ}}_{avg - opt} ≜ min_{f \in F} \underset{n \to \infty}{lim sup} \frac{\sum_{i = 0}^{n - 1} E [A_{i} (Z_{i} + Y_{i + 1}) + \frac{m}{2} (Z_{i} + Y_{i + 1})^{2}]}{\sum_{i = 0}^{n - 1} E [Z_{i} + Y_{i + 1}]} \end{array} \end{matrix}

可以看出这里分子分母为 $Z_{i}$ 递增函数，因此 ${\bar{Δ}}_{avg - opt}$ 不随其单调递增，Zero-wait 并非最好策略

\begin{matrix} (17) & p (β) ≜ \min_{f \in F} \lim_{n \to \infty} \sup_{n \to \infty} \frac{1}{n} \sum_{i = 0}^{n - 1} E [(A_{i} - β) (Z_{i} + Y_{i + 1}) + \frac{m}{2} (Z_{i} + Y_{i + 1})^{2}] \end{matrix}

Lagrange！ $β$ 即分子分母的比

Lemma 3.5.

截图

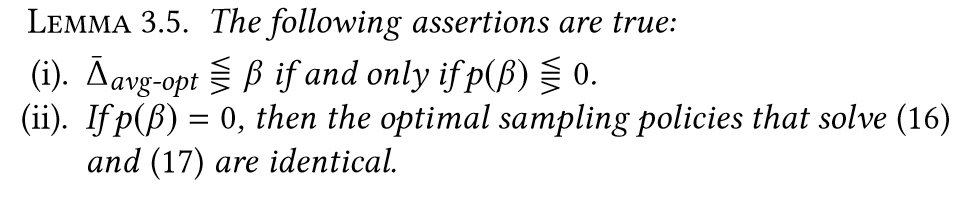
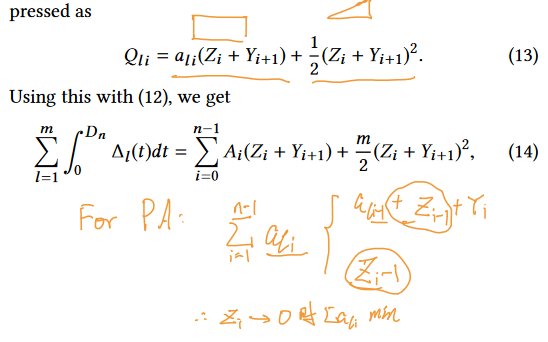
仿真

Notes

Memo

📘 Yin Sun
📘 Due to interference, only one source can be scheduledat a time
📘 minimizing the total average peak age (TaPA) and the total average age (TaA) of the sources
📘 separation principle: The optimalscheduling strategy and the optimal sampling strategy are independent of each other
📗 we prove that, for any givensampling strategy, the Maximum Age First (MAF) scheduling strategy provides the best age performance among all scheduling strategies
📗 While the zero-wait sampling strategy(in which a sample is generated once the channel becomes idle) isshown to be optimal for minimizing the TaPA, it does not always minimize the TaA
📗 we provide an approximate analysis of Bellman’s equation toapproximate the TaA-optimal sampling strategy by a water-fillingsolution

📘 Unlike traditional packet-based met-rics, such as throughput and delay, age is a destination-based met-ric that captures the information lag at the destination, and is hencemore suitable in achieving the goal of timely updates
📘 Last Generated First Served (LGFS)-type policies are (nearly) opti-mal for minimizing any non-decreasing functional of the age pro-cess in single flow multi-server and multi-hop networks.
📘 generate-at-will"model [2, 31, 32, 35, 41], in which the generation times (samplingtimes) of the update packets are controllable
📗 Our investigation in this paper reveals that the zero-wait sampling strategy does not always minimize the age (the TaA in particular) in multi-source networks with random transmission times (which could be more than one time slot)
📗 finding the optimal policy thatcontrols the sampling and scheduling strategies to minimize two age of information metrics
📗 We formulate the optimal sampling problem for minimizing the TaPA
📗 Hence, theMAF scheduling strategy and zero-wait sampling strategyare jointly optimal for minimizing the TaPA (Theorem 3.4)
📗 minimizing theTaA into an equivalent optimization problem which thenenables us to use Dynamic Programming (DP) to obtain theoptimal sampling strategy
📗 there exists a sta-tionary deterministic sampling strategy that can achieve op-timality (Proposition 3.6)
📗 has a threshold property
📗 the relativevalue iteration (RVI) algorithm
📗 the MAF scheduling strategy and the threshold-based sampling strategy are jointly optimal for minimizingthe TaA (Theorem 3.8)
📗 approximate analysis ofBellman’s equation
📗 Because of the randomness of the trans-mission times, our model belongs to the class of semi-Markov de-cision problems (SMDPs)
📘 The channelis modeled as First-Come First-Served (FCFS) queue with randomi.i.d. service time Yi
📘 there is no need to generate an updatepacket during the busy periods

📘 the sourcescheduling strategy, denoted by π
📘 π , (r1,r2, . . .)
📘 ii) thesampling strategy, denoted by f
📘 f , (S1, S2, . . .), or equivalently, the sequence of waitingtimes f , (Z0, Z1, . . .)
📘 d = (π, f ) implies that a decisionpolicy d follows the scheduling strategy π and the sampling strat-egy f .

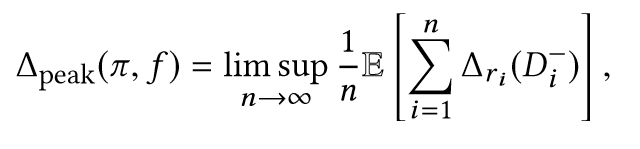
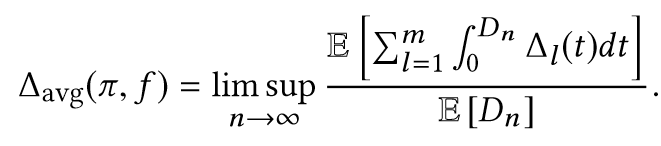
📘 Definition 3.1 ([14, 17, 18, 23, 34]). Maximum Age First schedul-ing strategy: In this scheduling strategy, the source with the max-imum age is served the first among all sources. Ties are brokenarbitrarily.

📘 it is not clear whether it also minimizes the TaA.This is because the latter metric may not be a non-decreasing func-tion of the waiting times as we will see later, which makes Problem (11) more challenging