离散时间Markov链

基本概念

（有限状态，finite states）

概述

Markov 链的提出，是为了验证大数定理可应用与不独立的随机变量序列中
独立性假设过于严格，往往不符合实际；因此允许时间节点间产生“有限”的联系，平衡实际与计算性

(离散) Markov 链

设 $X_{n}$ 是一个离散时间 Markov 链，则对于随机变量序列具有一阶记忆性，即转移概率质量函数满足

P {X_{n + 1} = a_{n + 1} | X_{n} = a_{n}, \dots, X_{0} = a_{0}} = P {X_{n + 1} = a_{n + 1} | X_{n} = a_{n}}

其中 $a_{n + 1}, a_{n}, . . ., a_{0} \in S$

例子

有限状态机（FSM）
例如手机就可以看作是一个有限状态机，其状态大致可以分为以下六个：关机、开机、待机、呼叫、通信、通信退出，手机的运作过程就是在这六个状态中切换的过程。
MIMO 预编码信道状态分类
假设接收机可以对这个信道矩阵进行估计并将估计结果反馈给发送端，便于发送端进行预编码发送。但是由于反馈信道的速率与资源是有限的，只能反馈信道的有限信息，此时需要将信道 $H$ 进行分类，假设可以分类为 $K = 2^{L}$ 种 $H_{1}, \dots, H_{K}$ ，此时接收机只需要反馈 L 比特的信息，发射机得到这个反馈信息，就可以判断此时的信道类型。

C-K 状态方程

状态概率： $p_{i} (n) = P {X_{n} = i}, \sum_{i = 1}^{N} p_{i} (n) = 1$
转移概率： $π_{i j} (m, n) = P {X_{n} = j | X_{m} = i}$ 即时刻 $m$ 下状态 $i$ 的条件下到时刻 $n$ 状态 $j$ 的条件概率
状态转移矩阵
$\begin{aligned} Π (m, n) & = [π_{i j} (m, n)]_{N \times N} \\ = [\begin{array}{cccc} π_{11} (m, n) & π_{12} (m, n) & \dots & π_{1 N} (m, n) \\ π_{21} (m, n) & π_{22} (m, n) & \dots & π_{2 N} (m, n) \\ \dots & \dots & \dots & \dots \\ π_{N 1} (m, n) & π_{N 2} (m, n) & \dots & π_{N N} (m, n) \end{array}] \\ π_{i j} (m, n) & ⩾ 0, \sum_{j = 1}^{N} π_{i j} (m, n) = 1 \end{aligned}$
Chapman-Kolmogorov (C-K) 方程
由全概率公式易求
$\begin{array}{r} P (n) = P (m) Π (m, n) \\ Π (m, n) = Π (m, r) Π (r, n) \end{array}$
即
$π_{i j} (m, n) = \sum_{k = 1}^{N} π_{i k} (m, r) π_{k j} (r, n)$

【意义】
从第 m 步的 i 状态转移到第 n 步的 j 状态的转移概率，等于所有可能转移路径的转移概率的和

平稳 Markov 链

齐次 Markov 链

$π_{i j} (m, n) = π_{i j} (n - m)$ 对任意 $i$ 和 $j$ 成立，也即转移概率 $π_{i j} (m, n)$ 只和时间间隔 $n - m$ 有关，和起点时刻 $m$ 无关的 Markov 链

对于齐次 Markov 链 $Π (m, n) = Π (n - m)$
因此 $P (n) = P (m) Π^{n - m}$

平稳 Markov 链

当齐次 Markov 链的状态概率矢量 $P (n) = P$ 为常矢量时，该 Markov 链为严平稳过程，简称平稳 Markov 链。

对于平稳 Markov 链，有

{\begin{cases} P = P Π \\ \sum_{i = 1}^{N} p_{i} = 1 \end{cases}

联立可求解平稳状态概率矢量 $P$

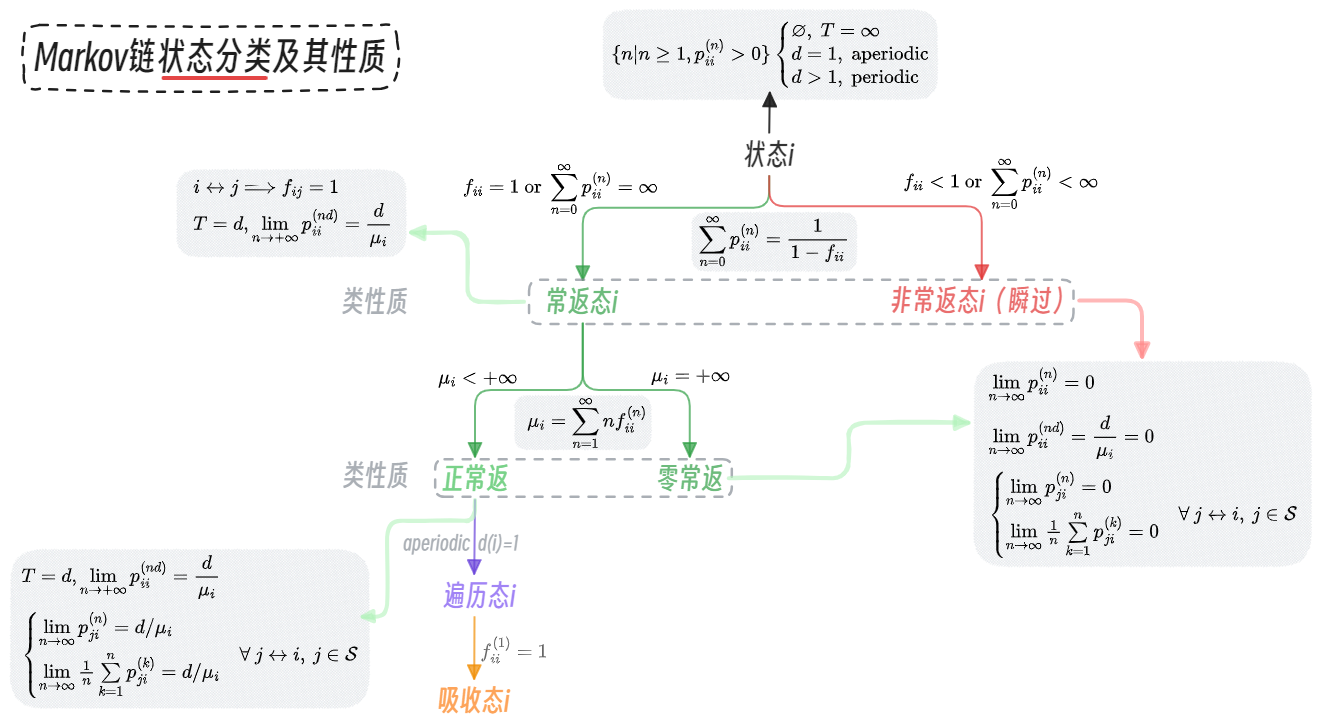
状态分类（常返|瞬过）

Markov链 2025-04-20 21.20.17.excalidraw

常返与瞬过

互达 (communicate)

可达 (accessible)

若存在 $n > 0$ ，使得 $π_{i j} (n) > 0$ ，则称状态 $j$ 是从状态 $i$ 可达的 (accessible)，记作 $i \to j$ ，它表示从状态 $i$ 经过有限步的转移可以到达状态 $j$

两个互相可达的状态 $i$ 和 $j$ 称为是互达的 (communicate)，记作 $i \leftrightarrow j$

【定理】
互达性是等价关系，也即满足

自反性： $i \leftrightarrow j$
对称性：若 $i \leftrightarrow j$ ，则 $j \leftrightarrow i$
传递性：若 $i \leftrightarrow j$ ，且 $j \leftrightarrow k$ ，则 $i \leftrightarrow k$

两个互达的状态，称为在一个状态类（class）中，互达将状态空间分割为诸多分离的类。若 Markov 链只有一个类，则称该链为不可约的（irreducible）。

由互达性定义，易证其性质

常返（recurrent）

令 $A (i)$ 是所有从状态 $i$ 可达的状态集合. 对于所有属于 $A (i)$ 的状态 $j$ ，状态 $i$ 也属于 $A (j)$ 。则状态 $i$ 是常返的。反之即非常返态（瞬过态）。

$n$ 步首达概率： $f_{i j} (n) = P {X_{n + k} = j, X_{n + k - 1} \neq j, \dots, X_{k + 1} \neq j | X_{k} = i}$
记迟早到达概率

f_{i j} = \sum_{n = 1}^{\infty} f_{j i} (n)

显然 $0 \leq f_{i j} (n) \leq f_{i j} \leq 1$
若 $f_{i i} = 1$ ，则状态 $i$ 为常返的；否则 $f_{i i} < 1$ 状态 $i$ 为瞬过的

说明：
若状态 $i$ 是常返的，则从状态 $i$ 出发，Markov 链将以概率 1 无穷次返回状态 $i$ ；若状态 $i$ 是瞬过的，则从状态 $i$ 出发，Markov 链无穷多次返回状态 $i$ 的概率是 0，也即 Markov 链只能有限次地返回状态 $i$ 。

常返或瞬过判别准则
状态 $i$ 是常返的充要条件是 $\sum_{n = 1}^{\infty} π_{i i} (n) = \infty$ 状态 $i$ 是瞬过的充要条件为 $\sum_{n = 1}^{\infty} π_{i i} (n) < \infty$

证明（瞬过充要条件）

令 RV $k$ 为过程返回 $i$ 的次数，则有

P {K = k | X_{0} = i} = f_{i i}^{k}, k = 1, 2, \dots

设随机变量 $I_{n}$ 为

I_{n} = {\begin{cases} 1, & X_{n} = i \\ 0, & X_{n} \neq i \end{cases}

因此

\begin{aligned} \sum_{n = 1}^{\infty} π_{i i} (n) & = \sum_{n = 1}^{\infty} P {X_{n} = i | X_{0} = i} \\ = \sum_{n = 1}^{\infty} E {I_{n} | X_{0} = i} = E {\sum_{n = 1}^{\infty} I_{n} | X_{0} = i} \\ = E {K | X_{0} = i} \\ = \sum_{k = 1}^{\infty} k P {K = k | X_{0} = i} \\ = \sum_{k = 1}^{\infty} k f_{i i}^{k} = \frac{f_{i i}}{(1 - f_{i i})^{2}} < \infty \end{aligned}

若状态 $j$ 是瞬过的，则对任意 $i \in S$ ，均有

lim_{n \to \infty} π_{i j} (n) = 0

状态空间分解定理

说明

一个马尔可夫链的状态集合可以分解成一个或多个常返类, 加上可能的一些非常返状态

一个常返态从它所属的类里任何一个状态出发是可达的, 但从其他类里的常返状态出发是不可达的

从任何一个常返状态出发都不可到达非常返状态

从一个非常返状态出发, 至少有一个 (可能有更多个) 常返态是可达的
由上述已知结果易得出下列定理

状态空间 S 必可分解为

S = N \cup C_{1} \cup C_{2} \cup \dots \cup C_{k} \cup \dots

其中 $N$ 是瞬过状态的集合， $C_{1}, C_{2}, \cdot \cdot \cdot, C_{k}, \cdot \cdot \cdot$ 是两两互不相交的由常返状态组成的闭集，且满足如下条件：

对每一 $k$ ， $C_{k}$ 内任意两个状态是互达的。
对任意 $k = 1$ ，和任意 $i \in C_{k}$ 和 $j \in C_{l}$ ， $i$ 和 $j$ 互不可达。

状态空间分解举例

通过状态转移矩阵进行状态分解

Π = (\begin{array}{cccc} 1 / 2 & 1 / 2 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 / 2 & 0 & 1 / 4 & 1 / 4 \\ 0 & 1 / 4 & 1 / 4 & 1 / 2 \end{array})

状态空间为 $S = {0, 1, 2, 3}$ ，其中状态 2,3 为瞬过态，等价类为 ${0, 1}$ 。状态分解为 $S = {0, 1} \cup {2, 3}$
|170

常返态的性质（常返|周期|遍历）

正常返&零常返
通过首次返回状态 $i$ 的期望部署判断正常返/零常返

正常返&零常返

$m_{i} = \sum_{n = 1}^{\infty} n f_{i i} (n)$

显然， $m_{i}$ 是首次返回状态 $i$ 的期望步数，称为状态 $i$ 的平均常返时
若 $m_{i} = \infty$ ，则称状态 $i$ 是零常返的； $m_{i} < \infty$ 时，称状态 $i$ 是正常返的

\underset{n \to \infty}{l i m} π_{i i} (n) = \frac{c}{m_{i}}

其中 $c$ 为常数。若 $l i m_{n \to \infty} π_{i i} (n) = 0$ 则该状态零常返；若 $l i m_{n \to \infty} π_{i i} (n) > 0$ 则该状态正常返

常返态的周期
揭示了常返状态返回自身的周期规律

周期性 (periodic)

【定理】
设 $i$ 为 Markov 链的一个常返态，使 $π_{i i} (n) > 0$ 的所有 $n$ 的最大公约数称作状态 $i$ 的周期，记 $d (i)$

易证若 $i \leftrightarrow j$ ，则 $d (i) = d (j)$

一个常返类是有周期的, 如果它的状态能被分成 $d > 1$ 个相互不相交的子集 $S_{1}, . . . S_{d}$ ，且满足所有的转移都是从一个这样的子集到下一个即

\forall i \in S_{k}, p_{i j} > 0 \Rightarrow {\begin{cases} j \in S_{k + 1}, k = 1, . . ., d - 1 \\ j \in S_{1}, k = d \end{cases}

Example

Markov 链有一步状态转移矩阵

Π = [\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 / 2 & 0 & 1 / 2 & 0 \end{array}]

试求状态 1 的周期。

|400
由状态转移图可知，只有 $4, 6, 8 \dots$ 步时可从状态 1 重返回状态 1
或者通过计算 $π_{11} (k) k = 1, 2, \dots$ 可得上述结论。
由于 ${4, 6, 8, \dots}$ 最大公约数为 2，因此周期为 2.

【定理】若 $i \leftrightarrow j$ ，则 $d (i) = d (j)$ （因此一个常返类所有状态周期相同，周期具有类的性质，通常周期就指这个常返类的周期）

证明

$\begin{aligned} \exists m, n, k & π_{j i} (m), π_{i j} (n), π_{i i} (k) > 0 \\ ∴ & π_{j j} (n + m), π_{j j} (m + k + n) > 0 \\ d (j) | m + n, d (j) | m + k + n ⟶ d (j) | k, d (j) | d (i) \\ 同理 & d (j) | d (i) \end{aligned}$

如何确定一个常返类是非周期的

只需验证是否存在一个特定的时刻和特定的状态 ,使得经过 n 步以后, 可以到达 $R$ 中所有的状态

若一个常返类 $R$ 是非周期的，那么必 $\exists n, \forall i, j, π_{i j} (n) > 0$

遍历（ergodic）
一个非周期不可约的 Markov 链，若有一个状态是正常返的，则其所有状态均为遍历的，也称这个链是遍历的（有限状态）。
定理

若状态 $i$ 是遍历的，则有
$lim_{n \to \infty} π_{i i} (n) = \frac{1}{m_{i}} > 0$

其中 1 代表状态 $i$ 的周期， $m_{i}$ 代表平均常返时。若状态是周期为 $d$ 的正常返状态，则
$lim_{n \to \infty} π_{i i} (n) = \frac{d}{m_{i}} > 0$

那么 $lim_{n \to \infty} π_{i i} (n)$ 的意义即对于遍历链，当 $n$ 很大时，处于状态 $i$ 的概率，且此时与初始状态基本无关，即 $lim_{n \to \infty} π_{j i} (n) = lim_{n \to \infty} π_{k i} (n) = p_{i}$ 。称之为稳态概率。下面给出求解稳态概率方法

稳态收敛定理

对于遍历 Markov 链，状态 $j$ 与对应的稳态概率 $p_{j}$ 有下列性质：

$lim_{n \to \infty} π_{i j} (n) = p_{j} \forall i, j$
$p_{j}$ 是下列方程组唯一解

\begin{aligned} π_{j} & = \sum_{k = 1}^{m} π_{k} p_{k j}, j = 1, \dots, m, \\ 1 & = \sum_{k = 1}^{m} π_{k} . \end{aligned}

\begin{array}{r} p_{j} = 0, \forall t r a n s i e n t s t a t e s j \\ P_{j} > 0, \forall r e c u r r e n t s t a t e s j \end{array}

离散时间Markov链

基本概念

概述

C-K 状态方程

平稳 Markov 链

状态分类（常返|瞬过）

状态空间分解定理

常返态的性质（常返|周期|遍历）

常见模型

Markov 分支过程

Markov决策过程

隐 Markov 链

连续时间 Markov 链