整数编码

Is the standard binary representation for positive integers (e.g. $c_{b} (5) = 101$ ) a uniquely decodeable code ?

【动机】

任一（以终止符结尾）数据文件均可映射成一个（正）整数，因此若有对整数的 prefix code，则其也是对文件的 self-delimiting encoding。文件越大，其对应整数也就越大，难点在于整数范围，同文件大小一样，理论上是无穷的。

Denotation

The standard binary representation of a positive integer: $c_{b} (n) i . e . c_{b} (5) = 101$
The standard binary length of a positive integer: $l_{b} (n) i . e . l_{b} (5) = 3$
The headless binary representation of a positive integer: $c_{B} (n) i . e . c_{B} (5) = 01$

not a uniquely decodeable code
Since there is no way of knowing when an integer has ended. For example, $c_{b} (5) c_{b} (5) = 101101 = c_{b} (45)$

How to construct uniquely decodeable code for integers

这里整数编码是指对在二进制编码基础上实现唯一可译，而非指计算机中补码，反码等对数据的存储

对正整数唯一可译编码两种方案：

Self-delimiting codes.
传输 $l_{b} (n)$ 与 $c_{B} (n)$
Codes with 'end of file' characters.
编码为长度为 $b$ 的块，并预留 $2^{b}$ 个符号之一表示“结束”

Unary code

一元码，发送 n-1 个 0 和一个 1

码长： $l_{U} (n) = n$
最优时对应概率分布： $p_{U} (n) = 2^{- n}$

Self-delimiting codes

自定界符号码，对二进制编码长度进行编码，并生成一个自定界码

Code $C_{α}$

c_{α} (n) = c_{U} [l_{b} (n)] c_{B} (n)

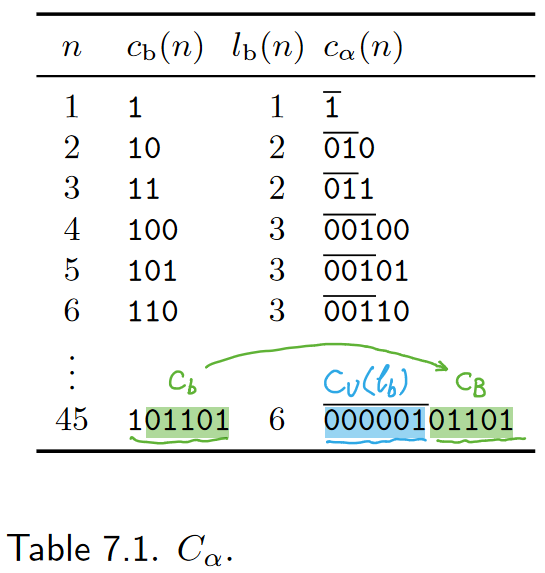
码长： $l_{α} (n) = 2 l_{b} (n) - 1 = l_{U} (l_{b} (n)) + l_{B} (n)$
最优时对应概率分布 $\begin{matrix} p_{α} (n) = P (l) P (n | l) \\ P (l) = 2^{- l}, P (n | l) = {\begin{cases} 2^{- l + 1} & l_{b} (n) = l \\ 0 & o t h e r s \end{cases} \end{matrix}$

最优概率分布近似 $\frac{1}{n^{2}}$
相比一元码，该码相对码长较短

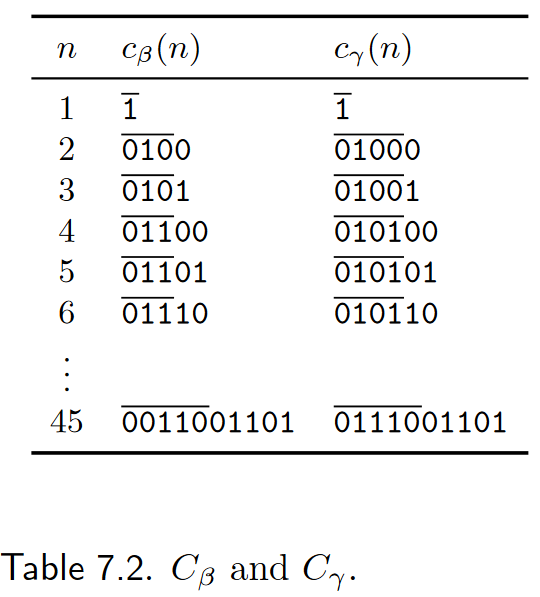
Code $C_{β}, C_{γ}, C_{δ} \dots$

当 n 较大时，编码长度近似于原始长度的 2 倍，显然看起来次优有大量冗余的，可以把对长度的编码通过 $C_{α}$ 缩短，形成一种 “递归”

Code $C_{β}$

c_{β} (n) = c_{α} [l_{b} (n)] c_{B} (n)

Code $C_{γ}$

c_{γ} (n) = c_{β} [l_{b} (n)] c_{B} (n)

Code $C_{δ}$

c_{δ} (n) = c_{γ} [l_{b} (n)] c_{B} (n)

Codes with end-of-file symbols

采用基于“字节”的表示（这里的“字节”表示任意固定长度字符串，不一定要 8bit）
一种高效的码如 $C_{15}$ ，表示将数字编码为 15 进制数，每个数位占 4bit (0000 — 1110)，并把 1111 作为终止符
类似上述思想易得基于形式 $2^{n} - 1$ 的任意进制整数码
These codes are almost complete(满足 Kraft 不等式). 如果考虑到编码整数 0 或空字符，则为 complete

Ex 7.1

Consider the implicit probability distribution over integers corresponding to the code with an end-of-file character.

If the code has eight-bit blocks (i.e., the integer is coded in base 255), what is the mean length in bits of the integer, under the implicit distribution?
If one wishes to encode binary files of expected size about one hundred kilobytes using a code with an end-of-file character, what is the optimal block size?

对于 base $q$ 的码，每个“字节”是终止符的概率为 $\frac{1}{q + 1}$ ，因此 $q$ 进制整数编码长度 $P (l_{q}) = {(\frac{q}{q + 1})}^{l_{q}} \frac{1}{q + 1}$ ，服从几何分布（?the prior to which this code is matched puts an exponential prior distribution over the length of the integer.）

$E (l) = q$ ，因此“字节数” $= q + 1 = 256$ ，编码期望长度为 $256 \times \log_{2} 256 \approx 2000$ bits
$100 K B = 800000$ bits, find q such that $q \log q \approx 800000$ bits, so 16-bit blocks are roughly the optimal size

Comparing the codes

any complete code corresponds to a prior for which it is optimal; you should not say that any other code is superior to it.
compare codes for integers is to consider a sequence of probability distributions, such as monotonic probability distributions over $n \geq 1$ , and rank the codes as to how well they encode any of these distributions
通用码
- A code is called a 'universal' code if for any distribution in a given class, it encodes into an average length that is within some factor of the ideal average length.
- 即所构造的码对一大类先验分布中任意一个均为很好的码
- 这里所考虑的先验分布通常要求：
  - 对整数分配单调递减概率
  - 有限熵分布

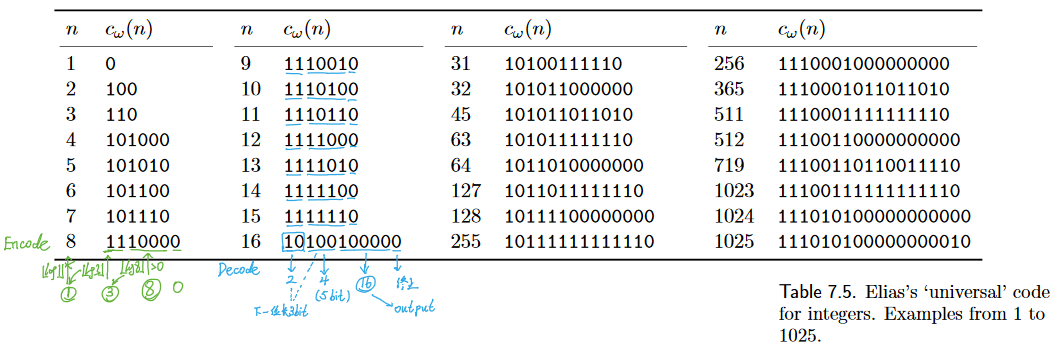
Elias's 'universal code for integers'

Algorithm Elias's encoder for an integer n.
Write '0' $Loop {$ If $⌊ \log n ⌋ = 0$ halt Prepend $c_{b} (n)$ to the written string $n : = ⌊ \log n ⌋$ $}$