关于推理

前置问题

Ex3.3 Inferring a decay constant

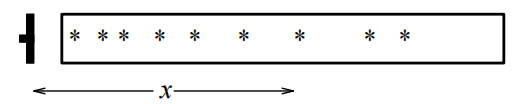
不稳定的粒子从一个源被释放出来, 并在距离 $x$ 处衰变, 其中实数 $x$ 是服从特征长度入的指数概率分布。只有发生在 $x = 1 c m$ 到 $x = 20 c m$ 的这个窗口内的衰变事件才能被观测到。假定在位置 $x_{\dots}, x_{N}$ 处观测到了 $N$ 次衰变， $λ$ 为多少?
|400

Ex3.4 Forensic evidence

两个人在一个犯罪现场留下了他们自己的血迹。对一个叫 Oliver 的嫌疑人进行检测, 并得出结果是“O”型血。两处血迹的血型查出来一处是“O”型 (这种血型在当地非常普遍，频度为 60%), 另一处是“AB"型 (这种血型非常罕见，频度为 1%)。这些数据 (在犯罪现场发现的“0”型血和“AB”型血) 是否支持“ Oliver 是两个出现在犯罪现场的人之一”的推测?

A first inference problem

@ Ex3.3:

类似问题：（某年数学建模）假设某市出租车有自身序号从 1 到 n，一段时间内随机观测路上出现的出租车并记录下其各自序号，如何估算本市出租车数量 n？

A couple of approaches
- constructing 'estimators' of the unknown parameters
- 'fitting' the model to the data
- a processed version of the data

....

The bent coin and model comparison

An example of legal evidence

下例表明贝叶斯推理可以给出先验概率以外更多信息

@ Ex3.4
Two people have left traces of their own blood at the scene of a crime. A suspect, Oliver, is tested and found to have type ‘O’ blood. The blood groups of the two traces are found to be of type ‘O’ (a common type in the local population, having frequency 60%) and of type ‘AB’ (a rare type, with frequency 1%). Do these data (type ‘O’ and ‘AB’ blood were found at scene) give evidence in favour of the proposition that Oliver was one of the two people present at the crime?

嫌疑犯与一个相对普遍的血型相同，能说明他更有可能在现场吗？

可以假设命题“该嫌疑犯与另一未知人士出现在现场”记作 $S$ ，“两个未知人士出现在现场”记作 $\overset{―}{S}$ 。案件先验知识为两个命题的先验概率比值 $P (D | S, H) / P (D | \overset{―}{S}, H)$

这里 $H$ 表示假设：两个人出现在现场中留下了血迹，且未知嫌疑犯血型概率分布与人群相同

\begin{array}{r} P (D | S, H) = p_{A B} \\ P (D | \overset{―}{S}, H) = 2 p_{O} p_{A B} \\ \frac{P (D | S, H)}{P (D | \overset{―}{S}, H)} = \frac{1}{2 p_{O}} \approx 0.83 \end{array}

上述结果给出了 Oliver 不在现场的较弱证明

虽然不太符合直觉，但改变下场景，考虑以下情形：

如果存在另一嫌犯Alberto，他的血型为 AB，那么凭直觉该嫌犯大概率是在现场的，事实上似然比展示结果也的确如此

\frac{P (D | S^{'}, H)}{P (D | \overset{―}{S}, H)} = \frac{p_{O}}{2 p_{O} p_{A B}} = 50

如果血型分布比率变为 99%O 型血；1%AB 型血。案发现场仍为一 O 型和一 AB 型血。那么现场检测出 O 型血如果有利于证实 Oliver 在现场，那么说明，几乎每个人都有更大的嫌疑！

If data provide evidence for some theories, they must also provide evidence against other theories.
如果现场有 10 个人血迹而非 2 个，当地 100 名居民中 90 位 O 型血，10 名 AB 型血
- 未知现场血型概率时，Oliver 在现场概率为 1/10
- 若已知现场血迹 9 个 AB 型，1 个 O 型，Oliver 出现在现场可能性增大了吗？
  
  没有！其出现概率变为了 1/90！
一般情形
假设案发现场出现 $n_{0}$ 个 O 型血和 $n_{A B}$ 个 AB 型；可怀疑人群共 N 人，其中血型分布分别为 $p_{O}, p_{A B}$
假设命题 $S$ ：Oliver（O 型血）与其他 $N - 1$ 个未知嫌疑犯在案发现场； $\overset{―}{S}$ ：未知 $N$ 个未知嫌疑犯在案发现场
则命题 $\overset{―}{S}$ 下的概率即从 $N$ 人中随机抽取 $n_{0}$ 个 O 型血和 $n_{A B}$ 个 AB 型， $S$ 即其他 $N - 1$ 抽取

\begin{array}{r} P (n_{0}, n_{AB} | \overset{―}{S}) = \frac{N!}{n_{0}! n_{AB!}} p_{0}^{n_{O}} p_{AB}^{n_{AB}} \\ P (n_{0}, n_{AB} | S) = \frac{(N - 1)!}{(n_{0} - 1)! n_{AB}!} p_{O}^{n_{O} - 1} p_{AB}^{n_{AB}} \\ \frac{P (n_{O}, n_{AB} ∣ S)}{P (n_{O}, n_{AB} ∣ \bar{S})} = \frac{n_{O} / N}{p_{O}} \end{array}

上式说明 Oliver 是否出现在现场问题的贡献仅取决于他的血型在观测数据中频度与人群中频度的比较，与其他血型数据无关！