Dinkelbach算法

问题描述

在 $N$ 个物体中选择 $K$ 个物体，使得总收益与总代价比最大化：

max_{S \subseteq {1, . . ., N}, | S | = K} \frac{\sum_{i \in S} v_{i}}{\sum_{i \in S} c_{i}}

$v_{i}$ ：第 $i$ 个物体的收益（如热量）
$c_{i}$ ：第 $i$ 个物体的代价（如价格）
$S$ ：选中的物体集合

问题转化思路

目标函数调整
令最优比值为

r = \frac{\sum_{i \in S} v_{i}}{\sum_{i \in S} c_{i}}

则有

\sum_{i \in S} v_{i} - r \sum_{i \in S} c_{i} = 0

构造函数
定义辅助函数： $F (r) = \sum_{i \in S} v_{i} - r \sum_{i \in S} c_{i}, | S | = K$ 则该函数满足： $f (0) \geq 0, f (r_{max}) \leq 0$ 。
由于仅 $r$ 一个变量因此 $F (r)$ 在平面坐标系上体现为一条直线，每组 $S$ 都分别唯一地对应一条直线，这些直线的截距均 $\geq 0$ 、斜率均 $\leq 0$ 。而截距的最大值就是我们要求的 $R = max_{| S | = K} r$ 。

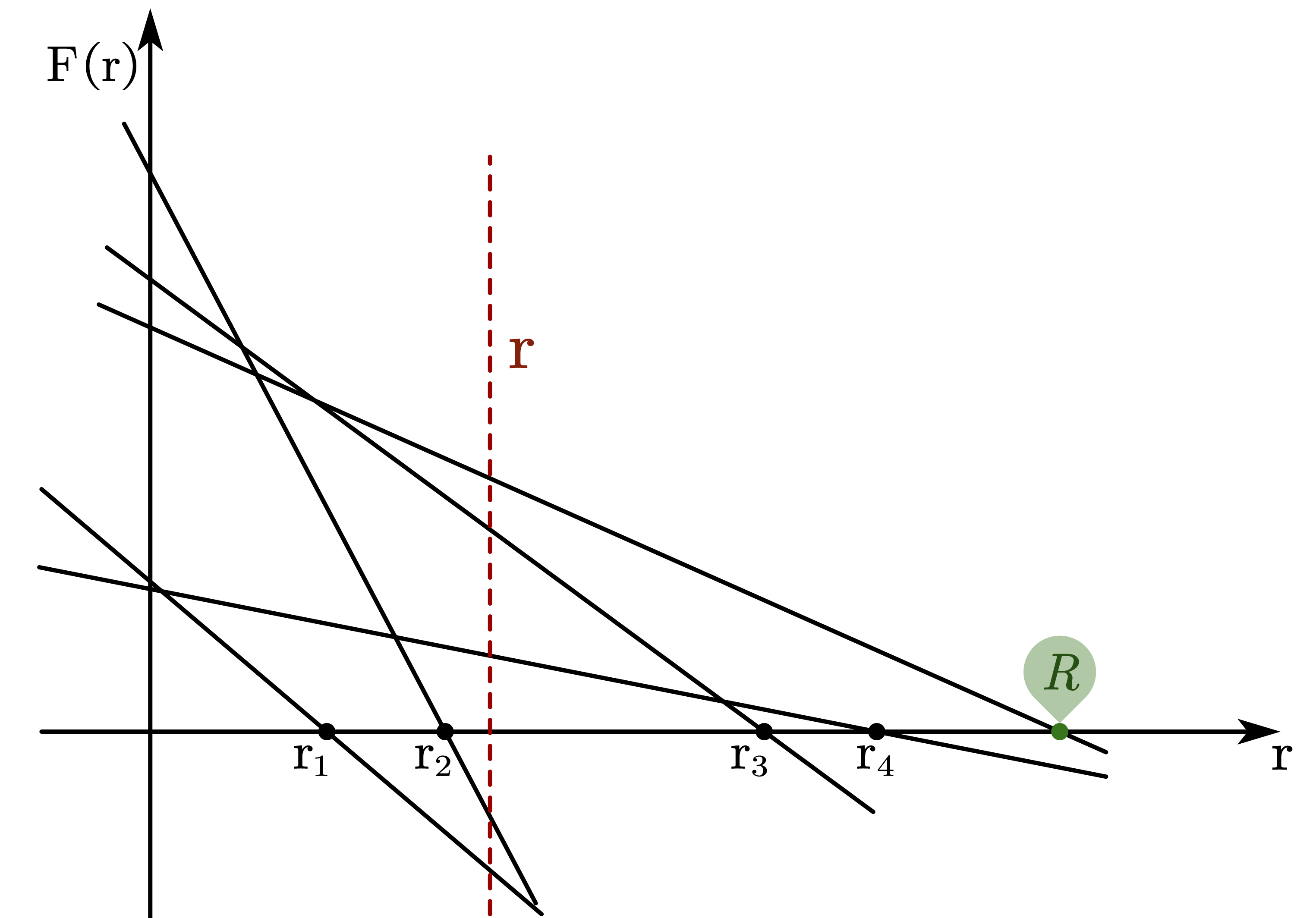
因此可以通过 $max F (r)$ 判定，若大于 0 说明 $r < R$ 反之说明 $r > R$ ，且 $max F (R) = 0$

如何求 $max F (r)$

那么首要的问题便是如何在给定 $r$ 时求出

max_{S} F (r) s . t . | S | = K

因为 $r$ 已知所以 $v_{i} - r c_{i}$ 其实已经确定了，那么可以记 $u_{i} = v_{i} - r c_{i}$ ，则选取 $K$ 个最大的 $u_{i}$ 即为 $max_{S} F (r)$

二分法

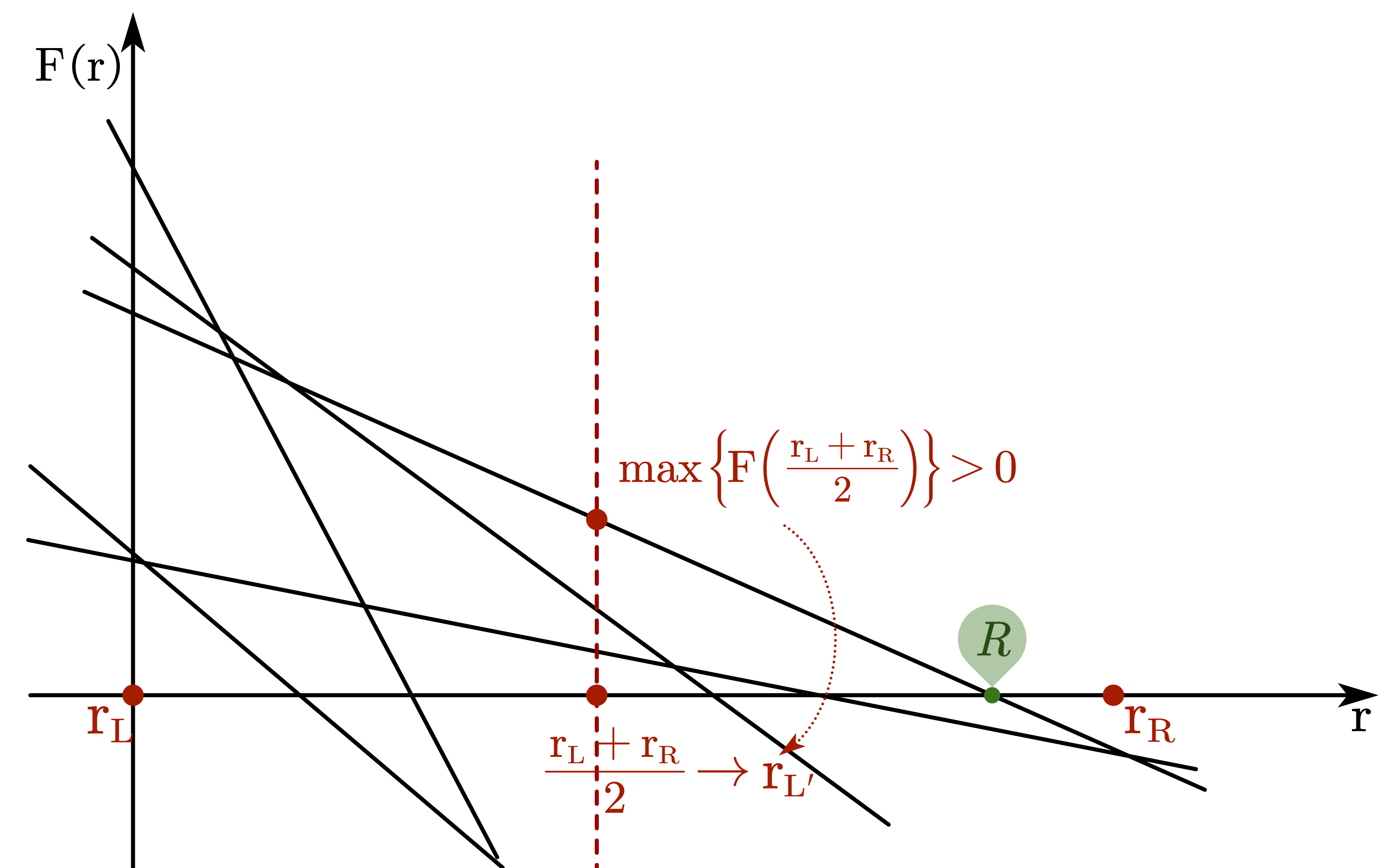
Dinkelbach算法

传统二分法仅用 $F (r) > 0$ 条件调整搜索区间，但忽略了关键信息：当 $F (r) > 0$ 时，其对应的零点值本身就是更优解。

如图随意选取一个 $r$ ，找到当前的 $max F (r)$ 所在的直线，移动到 $r^{'}, r^{″}$ 上面去，这样做甚至只要2步即可到位）

【优势】

直接利用F(r)>0时的R值信息
避免盲目二分，加速收敛
保证找到全局最优解

参考

Dinkelbach是什么算法？ - 知乎

© 2024 LiQ :) 由 Obsidian&Github 强力驱动